Search Algorithms for Chess Engines
Building a Chess Engine - Part 5
Now that basic move generation is (hopefully) done, it's time to work on the two most exciting parts of the engine, the evaluation and search.
I wasn't sure with which I should start, since the search needs and evaluation function to work. But if one wants to tweak the evaluation function, search has to be already in place to test the changes to evaluation. I decided to start with search and I just wrote a simple evaluation function to test that everything is working. After search is done, I'll dive more into tweaking the evaluation function.
There are different algorithms to implement search, but in this post I'll focus on the standard method for chess engines, namely minimax search with alpha-beta pruning.
Minimax search
The minimax algorithm works by having two players, one which is trying to maximize the score (in chess that would be White) and one which is trying to minimize the score (this would be Black in chess). The players alternate and on each step they pick the move that achieves their goal of maximizing or minimizing the score. Hence the name minimax.
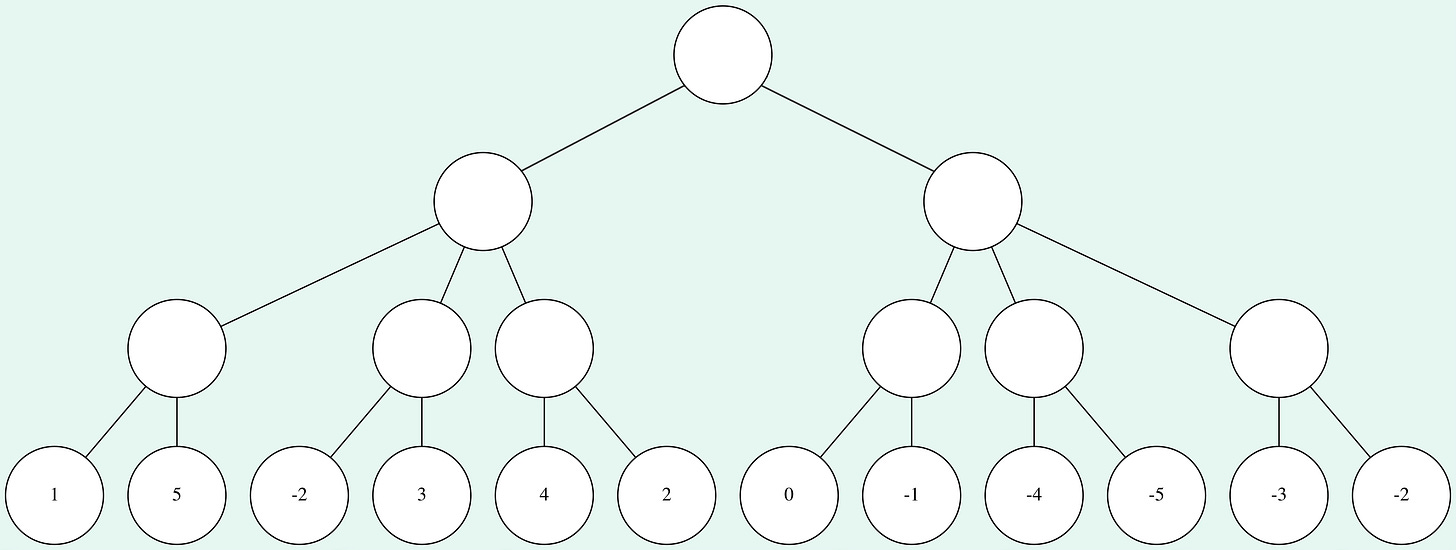
This is best illustrated with an example. The search is best represented by a tree, where the root node is the current position and each edge represents a move. The tree is built up to a certain depth, which is specified beforehand. To get an evaluation of the root node and the best move, the leaf nodes (nodes at the maximum depth) are evaluated first.
Then at each level in the tree, the nodes takes the lowest or highest value from all its child nodes, depending on whose turn it is. This is repeated until the starting position gets an evaluation and there is an optimal path through the tree.
In the example I assumed that it’s White to move in the starting position. So the first layer takes the maximum score of the nodes in the second layer, while the nodes in the second layer take the minimal score of the nodes in the third layer and so on.
Note that the final evaluation of the starting position is actually the evaluation of the leaf node, which will be reached by perfect play (according to the engine).
This algorithm works well, but the tree of variations grows exponentially, so using this algorithm alone for chess wouldn't be feasible.
There are many different pruning algorithms which aim to reduce the game tree. As you can imagine, removing variations from the calculations is a trade-off between speed and not cutting the best moves. I don't want to explore many different pruning algorithms now, but there is one pruning technique which always gives the same results as minimax search (meaning that the best variation will never be pruned) while also increasing the speed of the algorithm.
Alpha-Beta Pruning
This technique is called alpha-beta pruning and relies on a simple way to reduce the calculation of unnecessary variations. The way it works is quite intuitive.
Imagine that you are starting your calculation and you have different candidate moves. Suppose you went through all possibilities after the first candidate move and have determined that this leads to an equal position. Now you look into your second candidate move and your opponent has multiple answers to it. If the first response you look at leads to an advantage for your opponent, then you can simply discard your second candidate move, because it’ll be worse than your first candidate move. You don't have to look at the other moves to determine exactly how big the advantage for your opponent would be. It's enough to know that it's a worse option than your first candidate move.
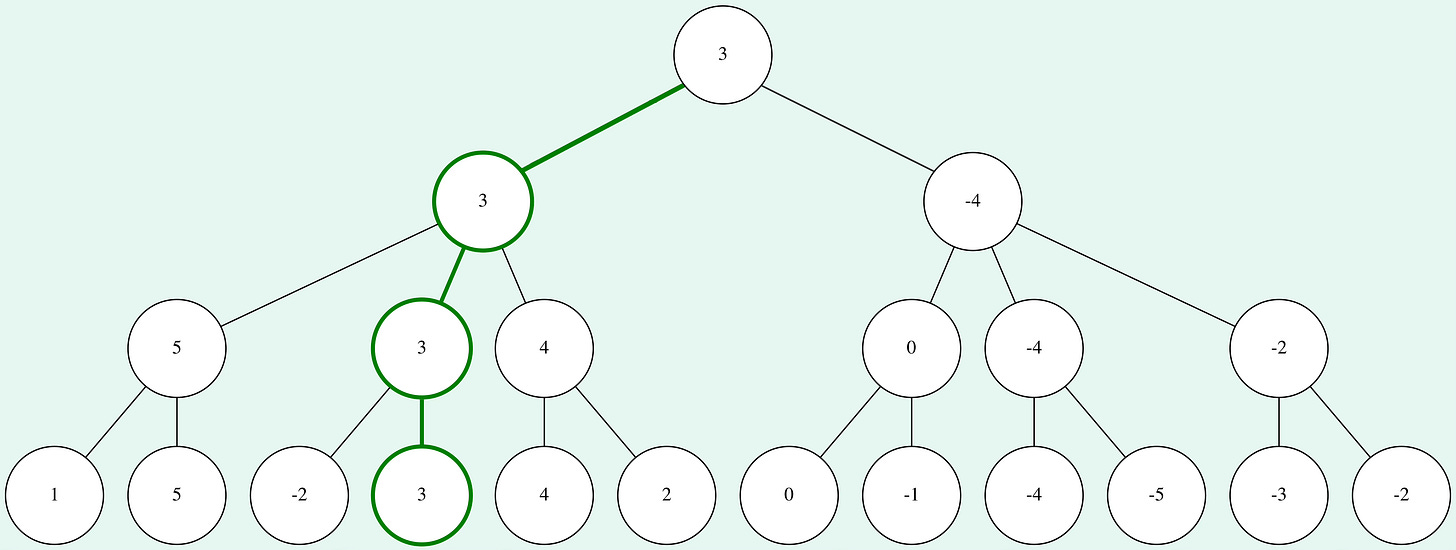
Alpha-beta pruning is the implementation of this thought for minimax search. Again, this is best illustrated by looking at the example from above. It's assumed that we go through the tree from left to right.

For the first 4 leaf nodes, everything worked the same way as with the minimax search. But as soon as the fifth leaf node is evaluated as 4, the algorithm can skip the evaluation of the last leaf node in that half of the tree. Since the node at depth 21 maximizes the score, we know that the value of the parent node will be at least 4. But since there is already a node evaluated with a score of 3 in the same depth, and the next parent node minimizes the score, we know that the node with a score greater or equal than 4 won't be chosen.
When looking at the second half of the tree, even more nodes can be pruned. As soon as we know that the node at depth 1 will have a score which is guaranteed to be lower than the first node at depth 1, we can skip all further calculations because the root node will choose the highest score (we assumed that it's White to move in the example).
As you can see, the score and optimal path through the tree remain unchanged, but we managed to prune nearly half the nodes. Alpha-beta pruning will always give the same results as minimax search and in general it'll save a lot of time.
How much time is saved, depends on the order in which the moves are calculated. In the worst case scenario where the moves are ordered from the worst to the best move, the two algorithms take the same amount of time. But in the best case scenario where the moves are ordered from best to worst, alpha-beta pruning will only need the square root of the time of minimax search. On average, the time taken will be somewhere between these two extremes.
As you can see, the move ordering has a huge impact on the speed and it's something I'll look into in the future.
Iterative Deepening
Usually engines have a time constraint when they calculate moves. The minimax algorithm isn't great in this case, since a search result isn't usable if the search has to be stopped early. So engines usually use an approach called iterative deepening.
This means that the engines first calculate with a depth of 1, then 2 and so on, until the time limit is reached. When the search for the current depth wasn't finished, the engine can simply use the calculations for the previous depth. So there will always be a full search result.
You might think that this is very inefficient, since many calculations have to be repeated. In theory this is correct, but the results from searches at lower depths can be used to order the moves for alpha-beta pruning. As mentioned above, this allows the algorithm to prune many variations which leads to a big speedup.
Next Steps
The end now seems near, but there a few more things to implement before the engine is working (and countless more things to tweak to increase the performance).
Next I’ll implement an evaluation function. Then I’ll work on implementing the UCI protocol so that the engine can be used with standard chess software. After a basic version is done, I’ll probably take a little break from the project before I’ll work on tweaking the engine to improve its playing strength.
I count the root node as depth 0


good choices. no information loss so far... (I assume that the move generation is not having anything else that reordering (premove stuff). And good idea to use a simple evaluation.
i think with ab pruning (math. equivalent to min-max), all the possible loss of information will be put on the evaluation function quality. Exhaustive search breadth and the quality seem to be in a trade off kind of optimization problem. The lower the quality the more leaf nodes to probe. I think one could argue that the min-max backbubbling might be actina as a multiplication of errors, and a max leaf eval has to be bigger than another one And another one, in a nested recursive fashion. But that is a not a mathematic argument yet. I am wondering if there would not be a toy caricature model that could illustrate some structure of leaf eval error model, and how the propagation works over the whole partial tree search optmizatoin. Even a single person binary decision game, might do. that is as far as I got a while ago. Anyway.. Yes the fun will be there.. and also any programmed bias.
You might also in your search get into the horzion problem, and the quiescense search extension is one of the traditional solutions. but if you intend to be real serious as SF seem to have geared, in focussing on improving the leaf functions given the chess-engine world of tournament pools defining what is the extent of chess positoins wilderness to be able to best play from, then, using the 1,3,3,5,9
eval might make you naturally find the quiecene search as the only attractive solution to the horizon problem.
And I think one might be forced to at least start that way. but to be conscious of what it might mean further down the line on the extent of domain sampling for that leaf function class (unless you fix all the parameters from your own expert guesses, or well use the others findings.
To go with that opinion, here is a possible suportting idea. SF is able to train its NN leaf eval, with SF+simple only, over any type of positions, not just quiescent. (and it is better being trained that way, to explore the full breadth of the SF+simple eval input output function training it.
As a complete search and leaf eval function of the root input position, SF+simple eval can score any position as its root input, only the non-user visible search from it will have to test for the leaf position quiescience. So NNue is actually learning to mimic SF+simple eval on shallower positions, than simple eval is finding worth min-max signal to backbubble in AB pruning or more aggressive stuff.
At some point one might consider that the NNue might become so good at detecting shallower more sublte signals, that even in "mexican standoff" or during a battle mid brawl not done, such signals could still be found.. That during play, one might not even need the simple eval.. I don't know where they have been in their exploration. It seems they are not wanting users to be aware of the inside story. I am priming myself to find out actualy. reading your updates. is good timing.
Also what are your thoughts about my ideas/questions.. any thing there sounding like I am missing some information you might have seen..