Now that the world championship match is over, I thought that it’s a good idea to take a final look back at the match as a whole. In previous posts, I looked at the individual games in some detail and now I’ll try to give an overview of the match as a whole.
Quality of Play
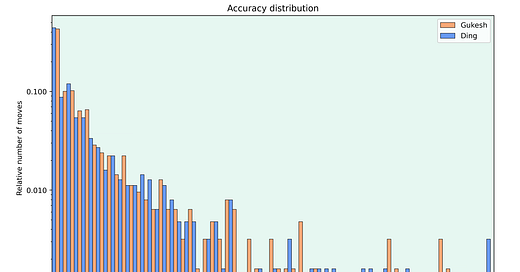
The most obvious thing to look at with engines is the quality of play. So I first looked at the move accuracies for both players.
The graph shows the relative number of moves made with each accuracy. Note that the y-axis is logarithmic.
Both players mostly played very accurately and there is hardly any difference in the number of moves they played with an accuracy higher than 80. But differences appear in the less accurate moves. Ding played more inaccuracies with an accuracy score between 55 and 65. Gukesh made a couple of more mistakes but this was offset by Ding’s 2 blunders in the match.
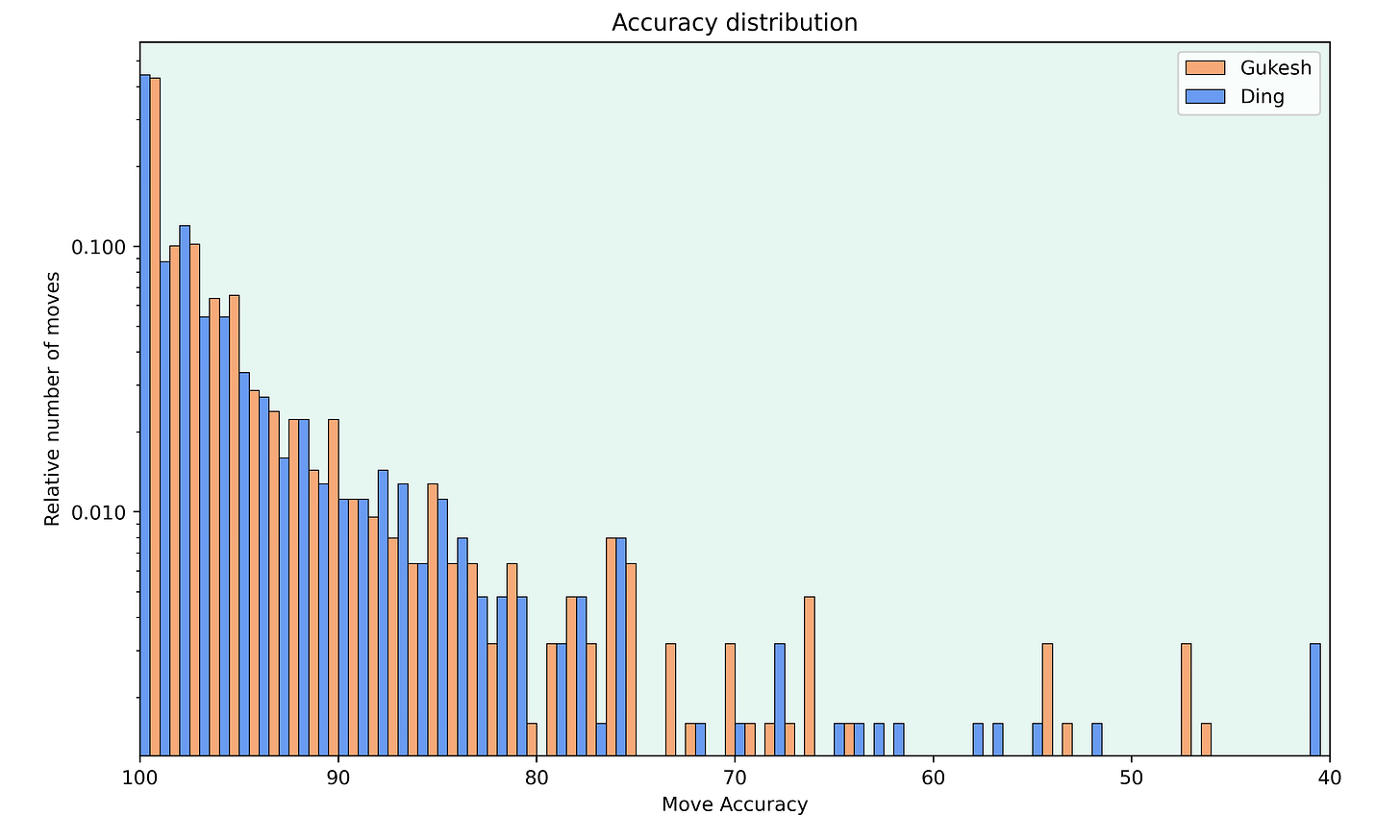
In addition to looking at how accurately the players played their moves, it’s also interesting to see how often they ended up in good or bad positions.
The graph shows the relative number of moves that Gukesh was much better (evaluation greater than +1), slightly better (evaluation between +1 and +0.5), equal (evaluation between +0.5 and -0.5), slightly worse (evaluation between -0.5 and -1) and much worse (evaluation below -1). Note that the graph for Ding would be the inverse of the graph above.
It’s surprising to see that Gukesh was more often worse than better, even though he won the match. This is because Ding lost games 11 and 14 due to blunders after which he resigned quickly, whereas Gukesh played on longer in the games he lost.
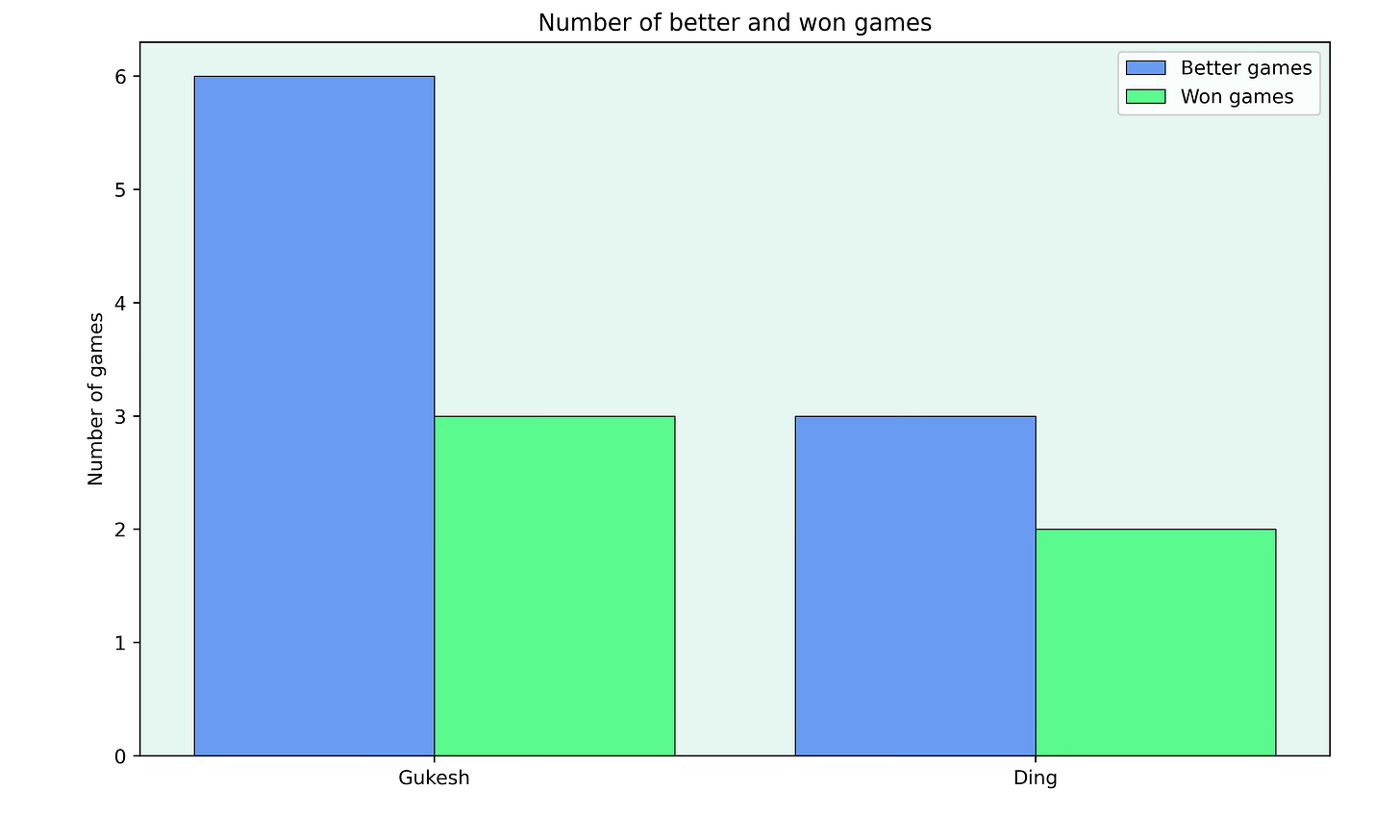
Finally, it’s also always interesting to see how well the players used their chances. To do this, I looked at the number of games where the players were much better (evaluation greater than +1) and the number of games the players actually won.
Gukesh was much better in 6 games but “only” managed to win 3 of these games. On the other hand, Ding has only failed to convert one game where he was much better.
Sharpness
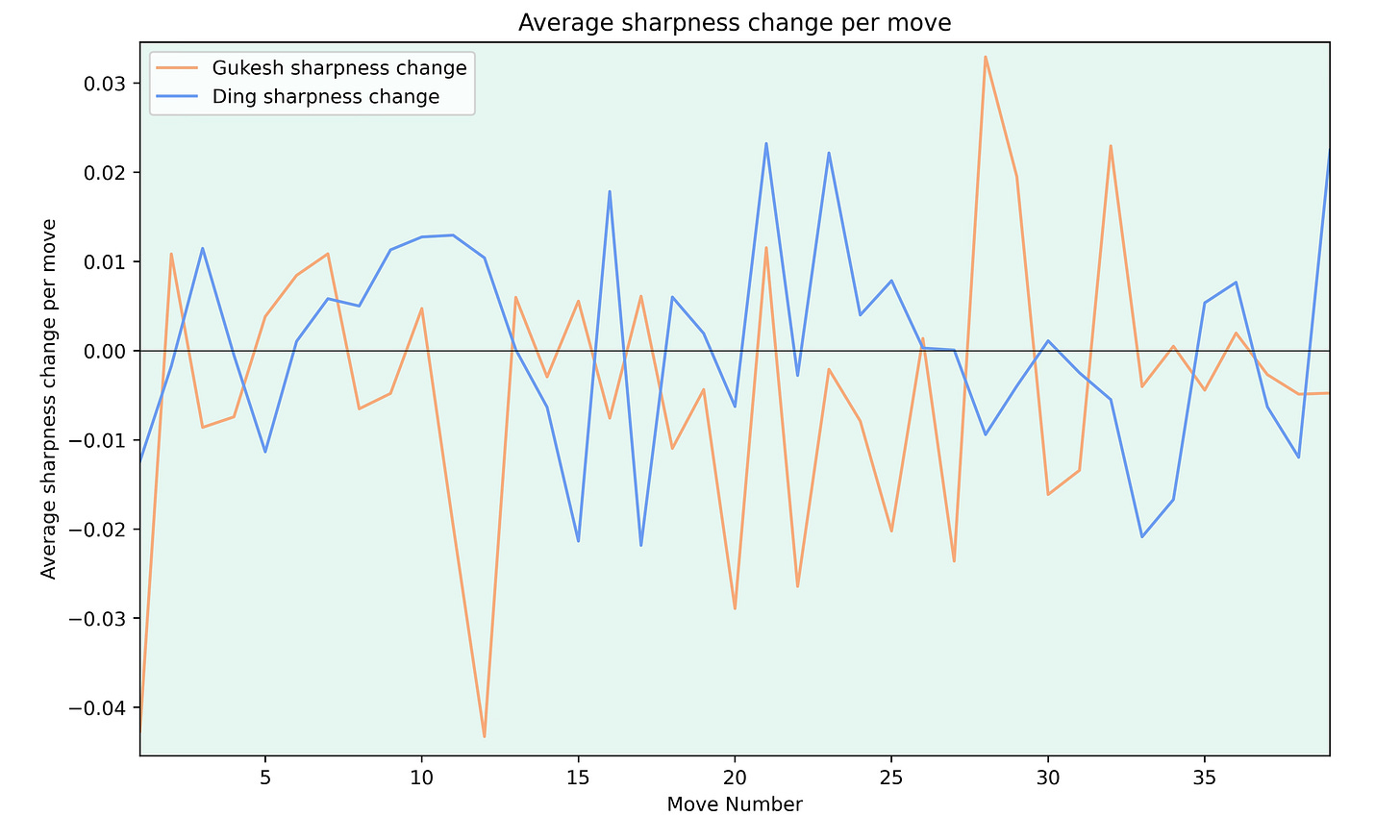
One thing I always like to look at is the sharpness of the games. To do this for the match, I calculated the average sharpness change on each move for both players.
To be honest, I don’t know how much one can take from a graph like this. But it shows that Gukesh tried to keep the games going between moves 25 and 35 while he played more calmly in the early middle game.
Clock Times
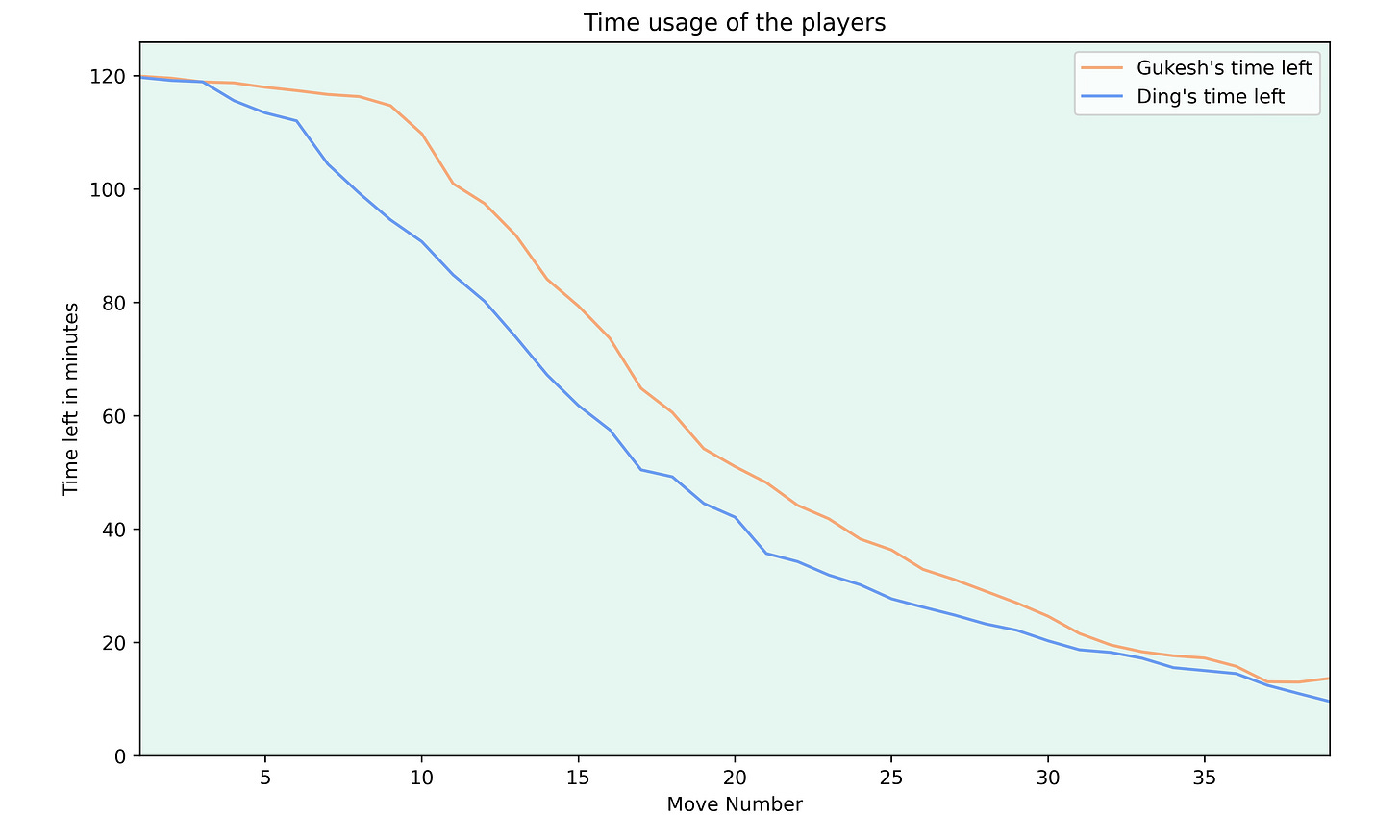
Another story about the match was Ding’s time usage early on in the games. When plotting the average time remaining for each player, one gets the following graph.
While Ding’s time usage looks much less extreme (this is due to some games that were played quickly from both players), it’s clear that Ding fell behind on the clock early on in the games and while he started to narrow the gap around move 15, he never quite caught back up with Gukesh’s time.
Conclusion
I would like to find a good way to get an overview of a match using just engines and without looking through individual games. While I think that the graphs above are a good start, I still feel that there is much room for improvement. So let me know what you would like to see added to make the overview more complete.



Could you make an Accuracy distribution graph but cumulative instead?
I understand the automatic goal as a way to figure out the feature space of games, you have augmented the usual move ceiling based only dimension inherited from engine pool ELO inferred back on any position of these ELO award winning tools game outcome populations, to the time control dimension (but how much of that is board chess), so not an increase of information about the core game made of position sequences. You have augmented it with the dimension of sharpness, as previously defined using more information about game continuations than the mere best move (or moves, but all best).
I think that we already are missing a lot of automatic analyses dimensions at the mere position level, then position pairs.. And then well whole games....
But you are asking the questions. There might be more information to include that would be valid at many games levels that could shed light automatically on any single game at some point. I think the territory from a one dimensional rating measure should be rather vast.
That one can't yet make sense on one new dimension like average sharpness change clocked on the ply. I noted that it was taken as a differential average (slope of sharpness at each pair of consecutive positions) over the sequence of positions. So perhaps human behavior is a bit volatile within the duration of the game, and there might be some windows average along the game in between the per position sharpness and then this whole game average. Sorry, that one can't yet, ... yadi yada... should be not disappointing. Perhaps we need to find more dimensions, but we could also dig into the definition/interpreation of shaprpness from its defining constituants.
But I wonder about human saturated high quality of chess relationship to the foundation of the sharpness definition. While coming from leela more generalist learner static evaluation function that in spite of the dilmemna of reinforcement learning might still retain a less tunnel vision chess position world view, it had to compromise on exploration as part of its glorious trajectory.
It is not clear to me what that RL compromise become quantitatively when they stop the engine learning improvement. About its whole combined RL batches set of games from when it was 100% generalist and legal chess uniform policy bias to whatever its satisfying expert level was. What is left in its static evaluation of the initial full exploration birth. (Uniform bias = no bias).
What does it mean, the WDL triplet (or pair of values) for a position? This is about the continuations from those position given a certain "tightness" of play, on either side (basically assumed the same, but which?). Perhaps being in the fog of that RL 2 prong pressure (exploration and exploitation, i.e. expertise gathering), one might use engine outside of the ELO optimal conditions. Go back to the stats of NN along their learning trajectories, and have their WDL points of view... Or force SF to the maximal of its multiple PV trhoughput.
But I think RL dilemma might also apply to human. The E. effect. At some point on makes some narrowing choices where their small (but famous and best of us) brains need to perform.. etc... and being single human life span (and small brain as all of us), well expertise comes at a cost. They might be threading always on sharper continuations than whatever mitigated LC0 many batches resultant evaluation function might still represent. I might be still not clear on interpretation of sharpness as defined previously, or on the definition itself. I mean my problem of understanding, not a critique at all.
I am perhaps missing a point. And I don't know where that leads. Just asking. Please do point out my possible misunderstandings or misconceptions I might have uttered.