In a previous post I looked at how well grandmasters score from positions where they have certain advantage according to Stockfish. This lead to an expected score depending on the evaluation which should reflect what happens in human games better than the centipawn evaluation.
Now I want to identify mistakes by calculating the expected score before and after a move was played and looking at the difference. If the expected score dropped more than 10 percent, the move is classified as a mistake. With this definition, around 4.3% of all moves played in the grandmaster games are mistakes.
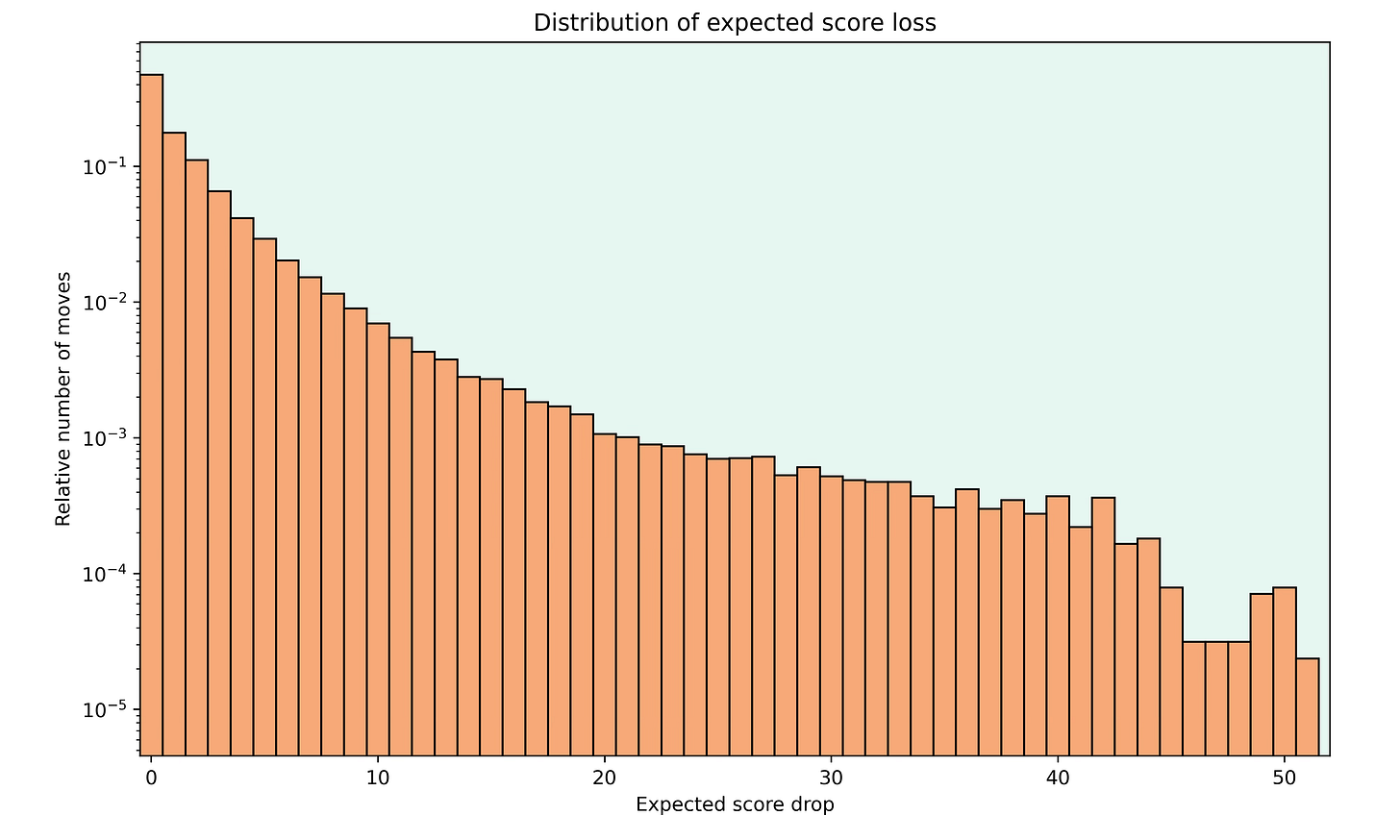
Here is the distribution of the expected score loss per move.
Note that the y-axis is logarithmic. As one would imagine, most moves have an expected score drop of 0, as grandmasters often play the best move. The frequency of expected score loss then decreases very quickly.
Now that we have defined mistakes, I want to see if some game situations lead to more mistakes.
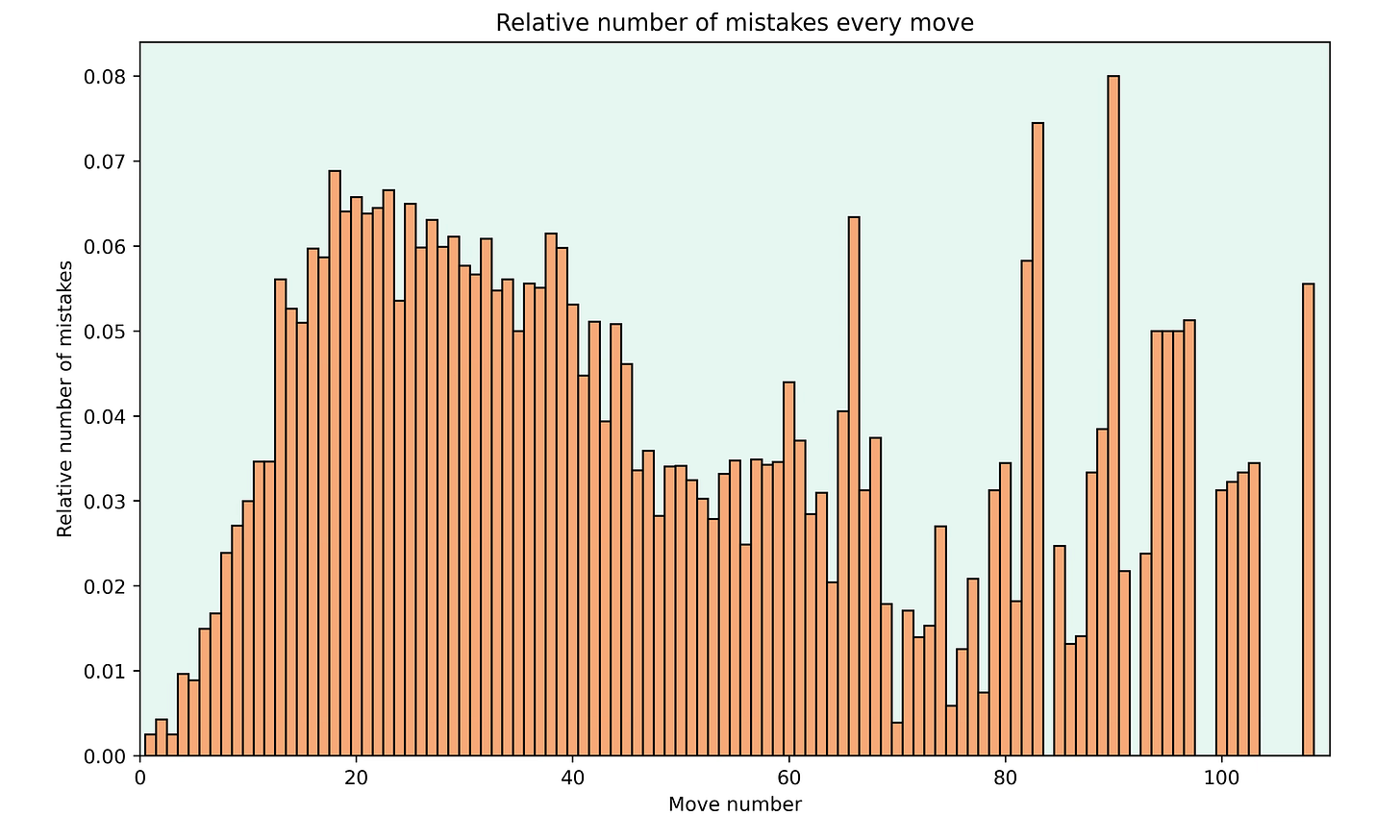
The famous move 40
Commentators often say that many mistakes happen at move 40, just as the players get extra time in most tournaments. I was interested in finding out if this is actually the case, so I calculated the relative number of mistakes the players made for each move number.
As one would expect, there are hardly any mistakes early on and most mistakes happen in the middlegame. The number of mistakes increases right before move 40 but there isn’t a particularly high number of mistakes exactly at move 40. Afterwards the number of mistakes decreases and as many games don’t go beyond move 60, the sample size gets smaller and it’s more difficult to make conclusions.
One reason for the increased mistakes at moves 35-40 is certainly the time situation. Unfortunately, the PGNs I used didn’t include time stamps but looking into the relation between quality of play and time left on the clock is something I want to do in the future.
Grouping Moves by Evaluation
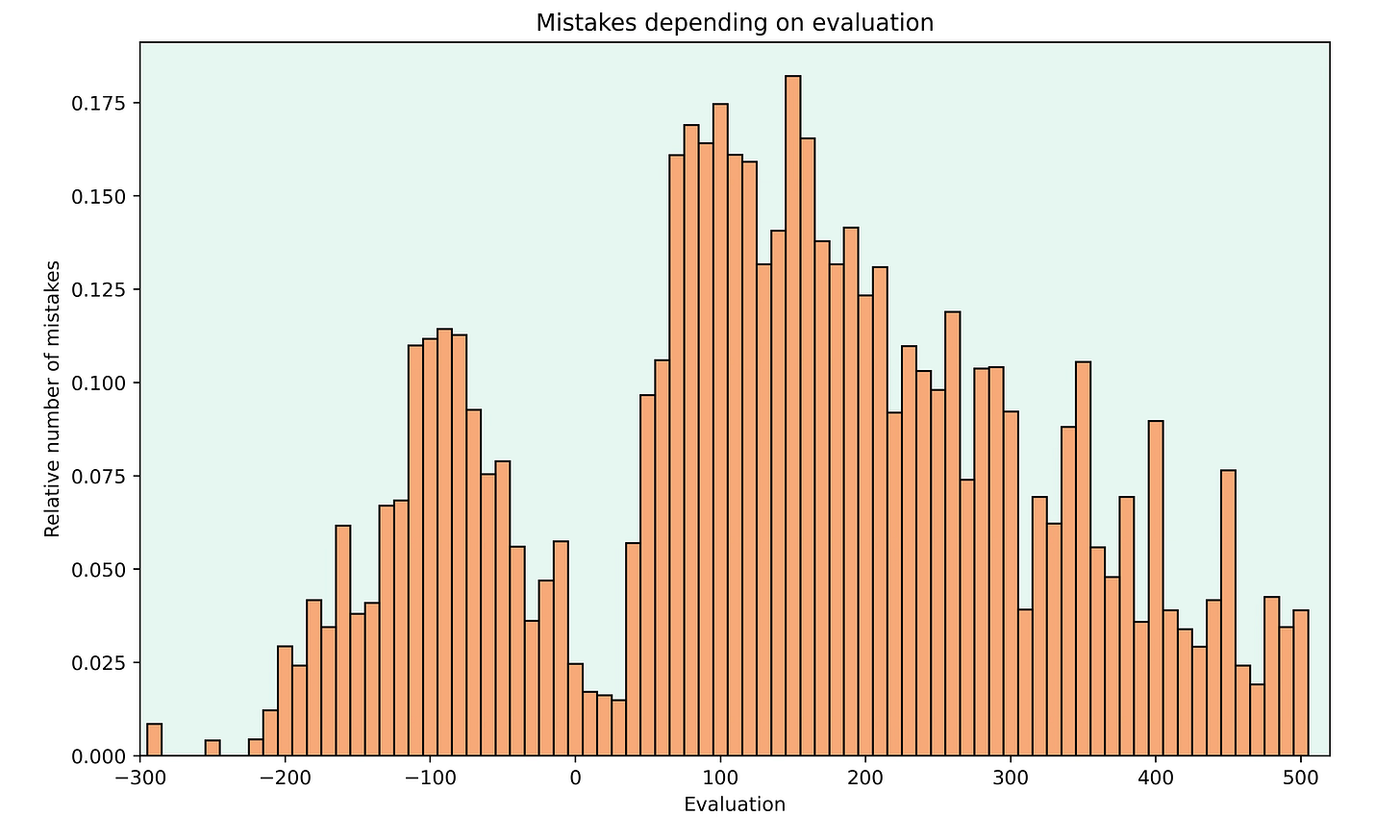
Another thing I wanted to look at is how the current evaluation affects the number of mistakes. To do this, I grouped the positions based on their evaluation from the perspective of the current side to move. Then I calculated the number of mistakes relative to the total moves played.
The first thing that jumped out to me was the asymmetry around equal positions. When players are slightly better, they make hardly any mistakes. But when they are standing slightly worse, mistakes happen much more frequently.
There are much more mistakes in positions where a player is slightly better. On the other hand, there aren’t as many mistakes when the evaluation is around -1. There are also fewer mistakes in very bad positions since the expected score is so low to begin with that not many moves reduce it by over 10%.
Future Ideas
The PGN files I used didn't have time stamps which means that I couldn't look at the remaining time or the move time to analyse the mistakes. This would certainly be interesting to look into for the future if I can find a good source for all files with the time stamps.
I also tried to quantify the sharpness of a position in the past and comparing this to the quality of play is certainly something I want to do in the future. But currently I'm thinking about different ways to refine sharpness and when I'm doing that I'll look at how it compares to the data from GM games.
Let me know if you have any other ideas for looking at the quality of play in these games.




Hi Julian,
Nice to read you again. I suggest to use the lichess approach for mistakes. It relies on the winning probability decrease, rather than the evaluation change. As the goal in chess is winning the game, their approach makes a lot of sense.
That last graph is so interesting! I'm trying to develop better intuition about this. Basically, the point is that from winning position you can go to equal, worse, or even losing, but from worse position you can only go to losing?
This makes a lot of sense mathematically, though I feel like it unduly overshadows your point about there being more mistakes from slightly better than from slightly worse positions, which is much more rooted in "popular imagination" / folk science. WDYT?