Creating an Accuracy Score based on GM Games
How can the quality of classical grandmaster games be calculated?
One thing that always bugs me when looking at the accuracy of classical games is that it’s rare to see a grandmaster game where both players had an accuracy below 90 and I’m unsure what the value of the accuracy should actually represent.
After trying to come up with a way to approximate the expected score in classical grandmaster games using Stockfish's evaluation, I want to use this score to calculate an accuracy that is designed to analyse GM games and where the scores have actual meaning.
Game Accuracy
To calculate the game accuracy, I calculated the average expected score loss (AXSL) per move for all the games in my dataset.
Distribution of expected score loss
Firstly I wanted to see how the average expected score loss is distributed. I got the following bar chart showing the frequency of each average expected score loss for the games in my dataset.
This distribution looks very nice. There are some outliers in both directions but overall it seems like the AXSL of most grandmaster games falls into a narrow band. I’ll use this average expected score loss per move to create the accuracy score.
Accuracy score from the data
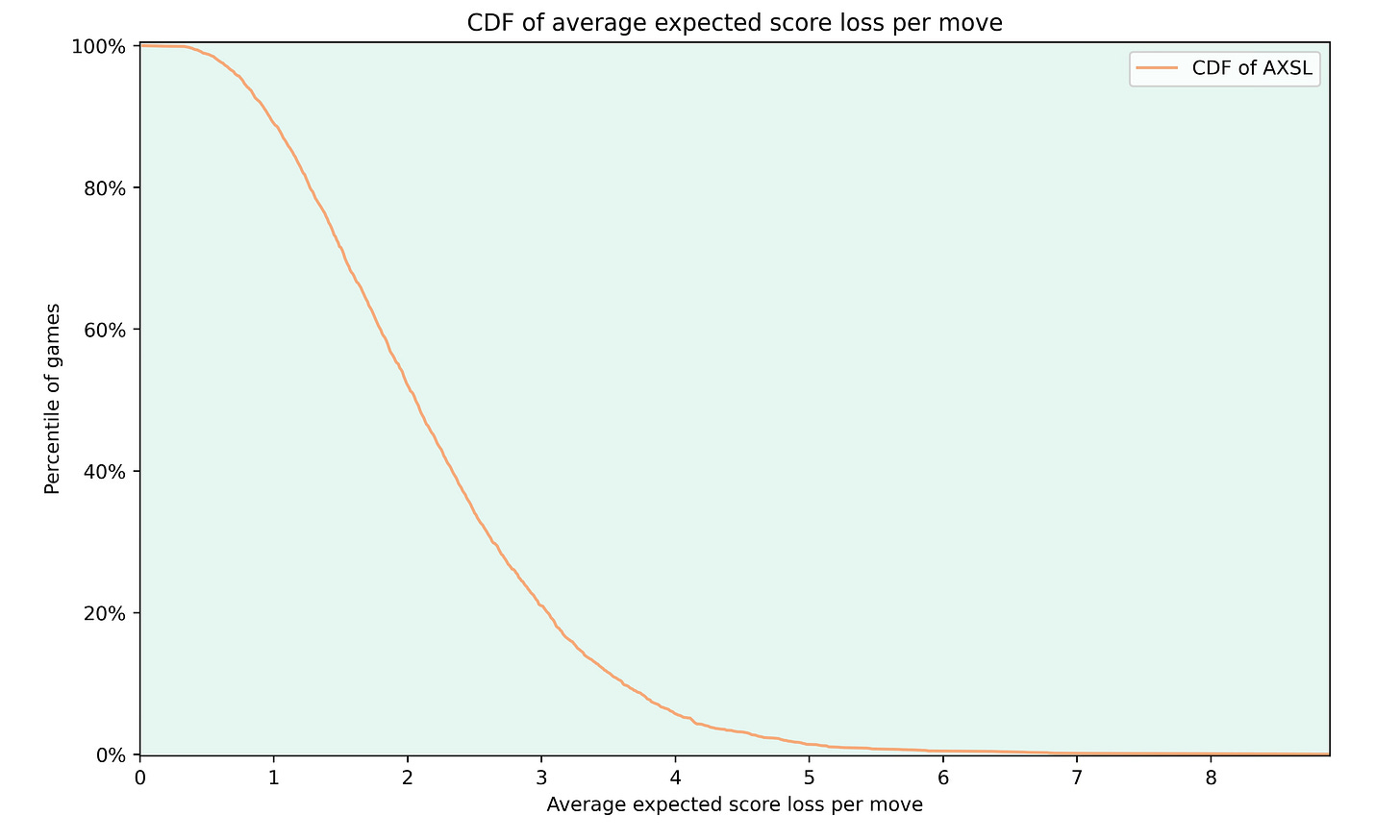
My idea for the accuracy is to see in which percentile the average expected score loss per move of a game was compared to the other games. So an accuracy of 90 should mean that the AXSL of a game is lower than the AXSL of 90% of the games played. To visualise this, I looked at the cumulative distribution function (CDF) and subtracted it from 100 which gives the following graph:
This looks like a very good candidate for an accuracy score. There are no sudden jumps in the CDF and the accuracy drops quickly to make high scores difficult to achieve.
Before finding a suitable function to represent this data, I wanted to test two things to see how the accuracy behaves for different types of games.
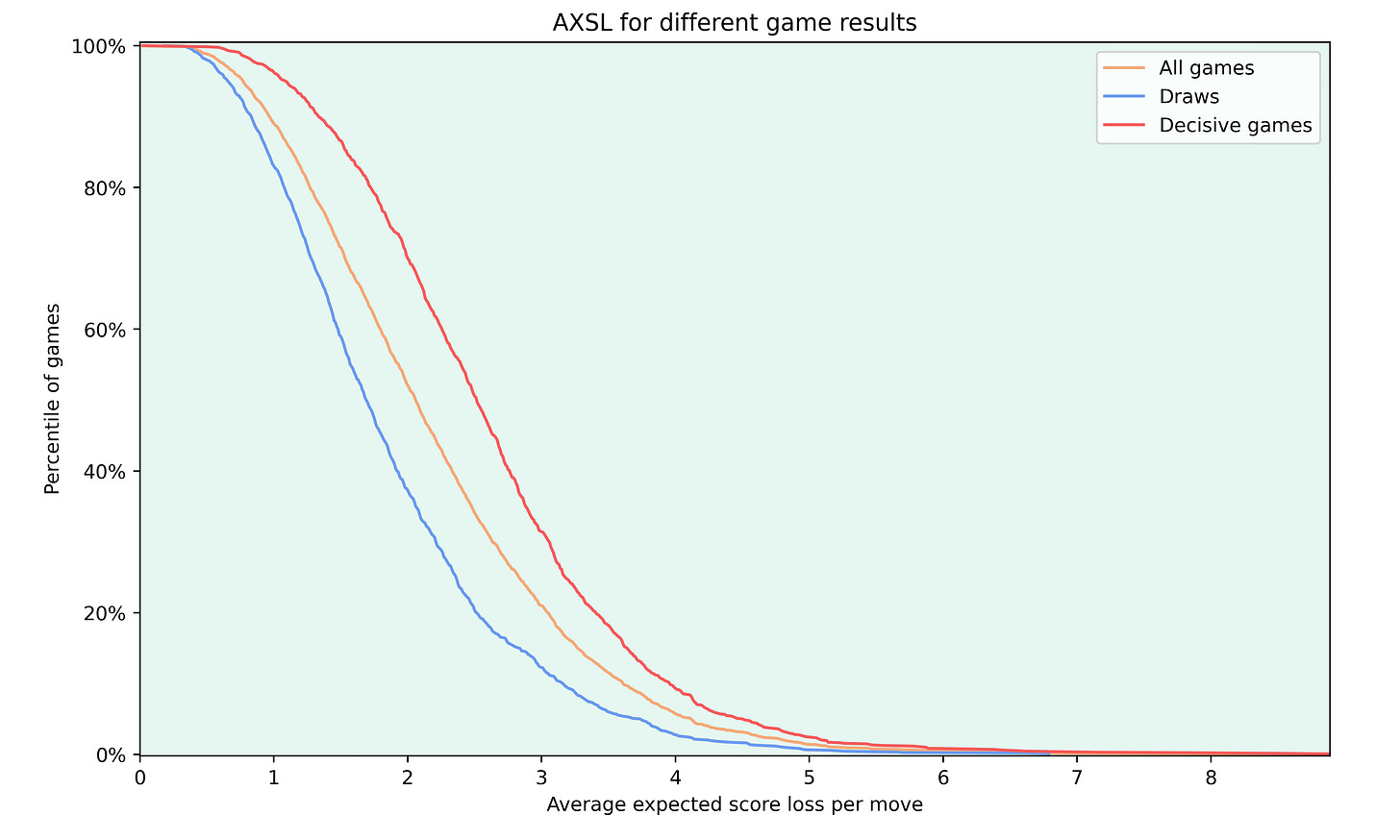
Firstly, I looked at draws and decisive games separately and compared them with the overall CDF.
As one would expect, drawn games are generally more accurate than all games and decisive games are less accurate. This makes total sense since one side has to make a mistake for a game to be decisive. One could also try and create an accuracy score only for decisive games or draws. I'm unsure how this could be used, but if you have any idea, let me know.
Secondly, I wanted to see how the game length affects the accuracy. Shorter games, especially short draws, usually give less opportunities for inaccuracies but long endgames may also lower the average expected score loss per move. So I didn't know what to expect before plotting the data.
Very short games may be a bit more accurate on average, but this could be due to short theoretical draws which should be nearly perfect games. But overall it seems like the game length doesn’t change the accuracy much. This is great because it means that one doesn’t have to think about the game length when looking at the accuracies of different games.
Fitting a function to the data
Finally, I want to find a function that represents the data I got from analysing the games and can be used to calculate the accuracy without using all the emperical data.
After some tests, I landed on the following function:
where I choose s=1.55. Note that I shifted x to the right by 0.25, so technically x has to be greater than 0.25. But for smaller values, one can simply set the accuracy to 100 as x represents the AXSL.
This function fits the data very well:
It’s actually quite difficult to see the line of the actual data behind the new curve.
Conclusion
I’m really happy with how the accuracy score came out, especially that the curve represents the empirical data so closely. I’ll use this score in the future and hope that it’ll prove useful when analysing GM games.
One shortcoming of this score is still that the accuracy between games varies a lot depending on the complexity of the game. I already did some work on that with a sharpness score in the past, but I want to revisit this and is possible change the accuracy to take the complexity of the game into account.
Let me know what you think about my approach to the accuracy score.