Quantifying the Control over Squares
What goes into controlling squares on the board?
Before starting with this project, I wanted to look into ways to quantify the piece coordination in a position. But as I started to think about that, I realised that an important part of piece coordination is how well they control the squares on the board. But it wasn't at all clear to me how to evaluate that. So I decided to focus on this problem first and work on piece coordination at some later time.
I tried to quantify the square control in a way that seemed logical to me, but if you have other ideas, please let me know. I'm also not entirely sure what factors should be included in piece coordination so I'm also happy to hear suggestions for that.
Defining square control
To quantify the control over a square, I want to assign a value ranging from -1 (total control for Black) to 1 (total control for White) to each square on the board. This turned out to be one of these problems that became harder and harder as I was thinking about it.
Pieces attacking squares
The first thing I realised is that determining which pieces attack a square isn't as trivial as it first appears. One thing to note is that pinned pieces shouldn’t contribute to the control of a square.
Another thing to keep in mind are batteries and connected rooks. Take the following position as an example:
The white rook on e1 isn’t directly attacking e8 but it should certainly be considered as controlling this square. The same goes for bishop-queen batteries.
So to get all pieces that are controlling a square, one also needs to check if there are any batteries on the board.
Calculating the control
After I determined which pieces were controlling a square, I needed to evaluate how much each piece contributes to the control.
Less valuable pieces are better at defending squares, as they can always capture a more valuable attacker, even when they get recaptured afterwards. So I felt that weaker pieces should contribute more to the control of a square.
I simply decided to take the reciprocals of the piece values, so a pawn has a “control value” of 1, knights and bishops of 1/3, rooks of 1/5, queens of 1/9 and for the king I took 1/12. There may be better values, I took these because I don’t really know how to test how good the values are.
To calculate the control of a square, I summed up all the values of the white pieces attacking that square and subtracted all values from the black pieces attacking it. This gave me one control score for each square on the board.
Examples
The score is probably best illustrated with examples, so take a look at the following position:
And here is how a heat map of the square control looks in this position:
One can clearly see the square that the white pawn controls and also the influence of white’s bishop. The control of the kings is more difficult to see as they have less influence over the squares due to the lower “control value”.
Note that the knight and bishop cancel each other out on the f7 and g6 squares as both are attacking it. So it looks as if these squares aren’t attacked by any piece.
Finally, let’s look at a middle game example. I thought that it would be particularly interesting to look at a position where one side has a weak colour complex, so I took the following example:
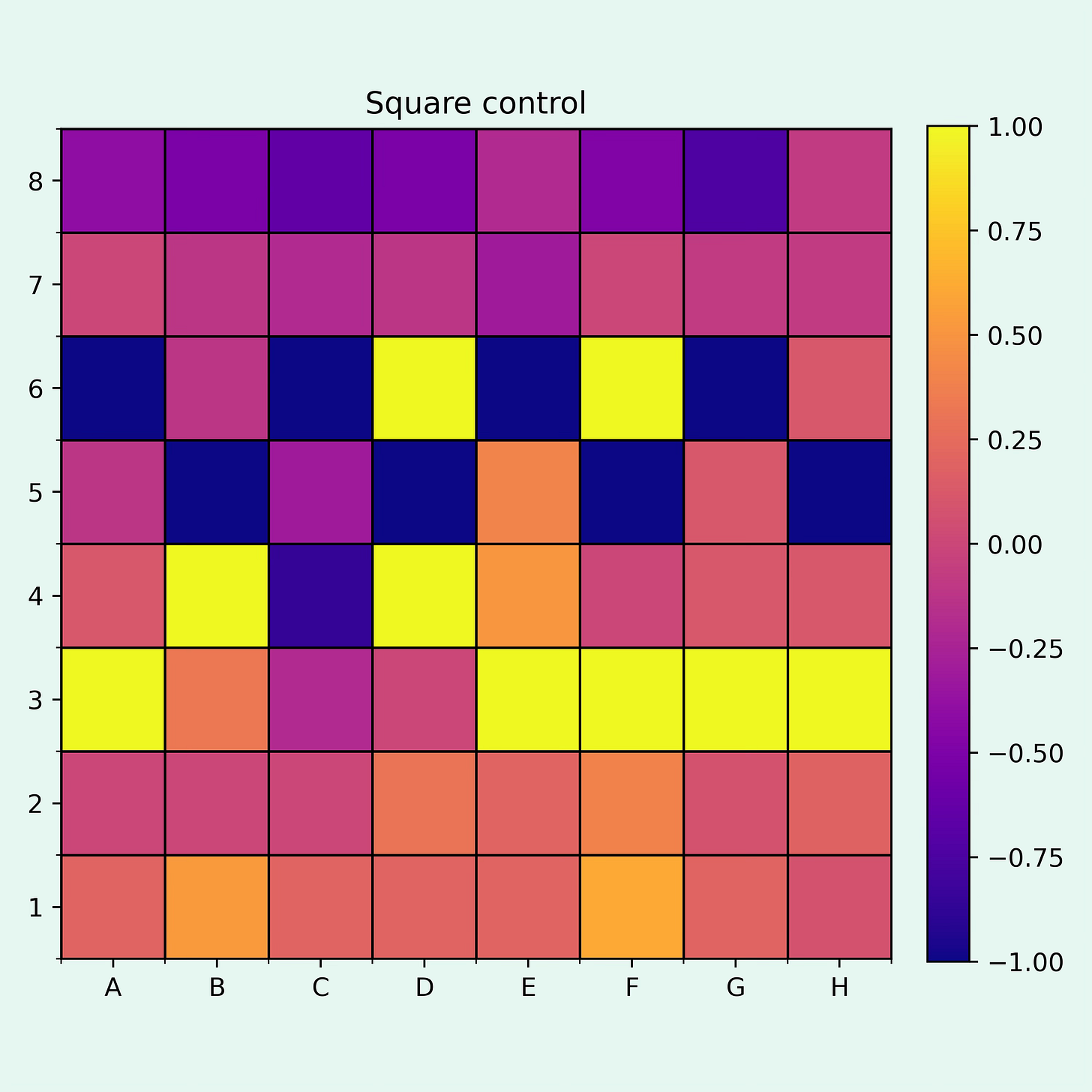
And here is the square control for this position:
As there are now much more pieces on the board, the heat map also looks wilder.
One can clearly see that all of black’s pawns are defending the light squares. This necessarily means that they leave the dark squares unprotected. The white pawn on e5 is controlling d6 and f6 while the queen attacks g5 and h6. Comparing the squares that the white and black pawns control on the kingside gives a good indication that black has problems with their dark squares.
Closing thoughts
I thought about splitting the control value I used into offensive and defensive control of the squares. The reason is that to occupy a square, a player needs to attack it one more time than the other player is defending it. So saying that a side controls a square depends on whether they want to attack or defend the square.
Also if one wants to determine which side has better control of the squares in general, it may be a good idea to value some squares more highly than others. For example, squares around the kings are much more important than many others. But how to compare the value of these different squares is also a difficult question.
Let me know what you think about the square control score and if you have any suggestions on how to quantify piece coordination.






The closing thoughts of determining the value of a controlled square makes me think of piece square tables in chess engines. They’re piece-specific, which I originally thought was a drawback but I think opens up some interesting analysis you can do of a position. For example if White has strong control over squares which have a high value in the knight’s piece square table, then in theory white should prioritize keeping his knights and black should prioritize fighting for those squares and trading off white’s knights.
Although I think the way the control calculation would have to function for something like this, is that control by a lower-valued piece is considered “absolute”. It doesn’t matter if my two knights, a bishop, both rooks and my queen are controlling a powerful square, if a pawn is defending it. I wonder if fixing this would be as easy as taking the squared reciprocal of the piece values instead?
Really interesting stuff, thanks for the post!