Move Generation for Sliding Pieces
Building a Chess Engine - Part 3
Last time I finished the move generation for pawns, knights and kings. Now only the sliding pieces, i.e. bishops, rooks and queens, are left to deal with. As mentioned before, this is a bit more tricky, since the moves might get blocked along the way. Generating the sliding moves takes a lot of fiddling with the bitboards. My main resources was this page from the Chessprogramming wiki and you can check it out if you want to dive deeper into the topic.
Overview
To generate the sliding moves, one needs to do a few calculations with bitboards, which individually aren't complicated, but at first it’s difficult to understand how they work together to generate the possible sliding moves. I'll illustrate everything with an example as we go along, for which I'll only use a 8 bit number to make everything easier to follow.
So suppose that our position is represented by the bitboard 10100101 and the piece we are interested in is the second one from the right, i.e. this is the piece where we want to generate the sliding moves. You can think of it as a rook that's moving along a rank and standing on the f-file. This bitboard might represent the following rank:
In the end, we want to get a bitboard where every square the rook can move to is set to 1, so it would be 00111010.
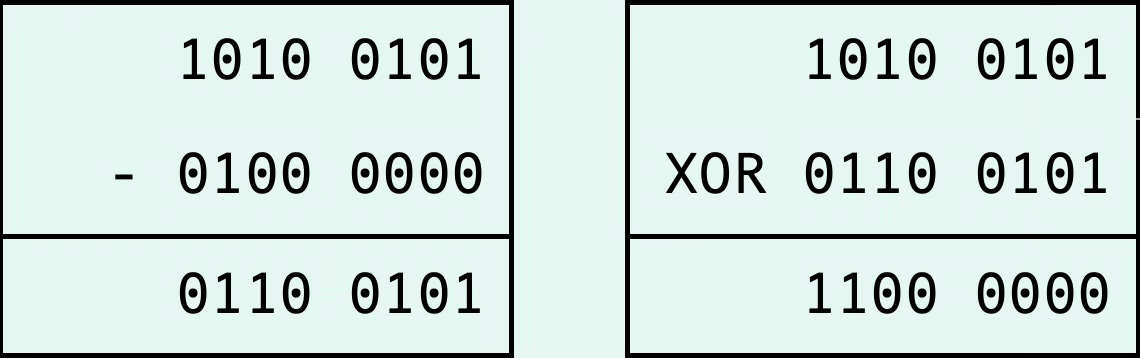
First we'll look at the moves to the left. We can move the rook until we hit a 1 while sliding over and then we need to check if we hit a friendly or enemy piece. So all bits until the first 1 (counting from the current piece to the left) should be set to 1.
At first it seems like this isn't easy to do, but one only needs to take the bitboard of the position and subtract 2 times the bitboard of the current piece. To multiply a binary number by 2, we just need to shift it 1 place to the left, so the bitboard of the rook (00000100) turns into 00001000. We get the following calculation:
Note how the 1s get carried in the calculation until we hit the first other piece along the rank.
Now we can take the result from this calculation and XOR it with the bitboard of the initial position:
As you can see, all bits cancel apart from the possible moves for the rook to the left, including the first piece it hits. In the end, we'll check if this is an enemy piece and if this isn't the case, the bit will get to 0.
But first we also need to generate the moves to the right. There isn't a neat trick like the subtraction from before, but one can simply take the bitboards and reverse them. The moves to the right from the initial bitboard are then the moves to the left in the reversed bitboard. The bitboard for the current piece also needs to be reversed when doing this. The required calculations are the following:
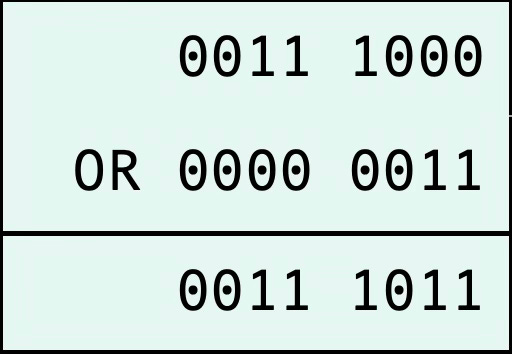
Now we need to put the two resulting bitboards together. The result from the reversed calculation needs to be reversed again to be oriented correctly in the end. The bitboards get put together with an OR:
Note that the pieces that got hit first are included in this bitboard. As mentioned before, one needs to clear the "captures" of friendly pieces. This is done by ANDing the result with the negated bitboard of all friendly pieces.
So finally we got the bitboard 00111010 which represents all possible moves for the rook along the rank.
Changes for whole positions
The move generation for a whole position happens in the way described above, but one needs to take a little care since not every piece on the board hampers the movement of a sliding piece.
Since a rook only gets blocked along the rank or file its currently occupying, one needs to remove all other pieces on the board before starting the calculations described above. To do this, one ANDs the initial position with the current rank (or file) of the rook, continues with the calculations as before and finally ANDs the result again with the current rank (or file) in order to remove any additional 1s that got added while doing the subtractions.
Movement along diagonals for bishops and queens is the same, one only needs to swap the current file and rank with the current diagonals the bishop (or queen) is occupying.
Implementation
After I wrapped my head around how all these calculations worked, the actual implementation wasn't too difficult, since the individual operations are quite straightforward.
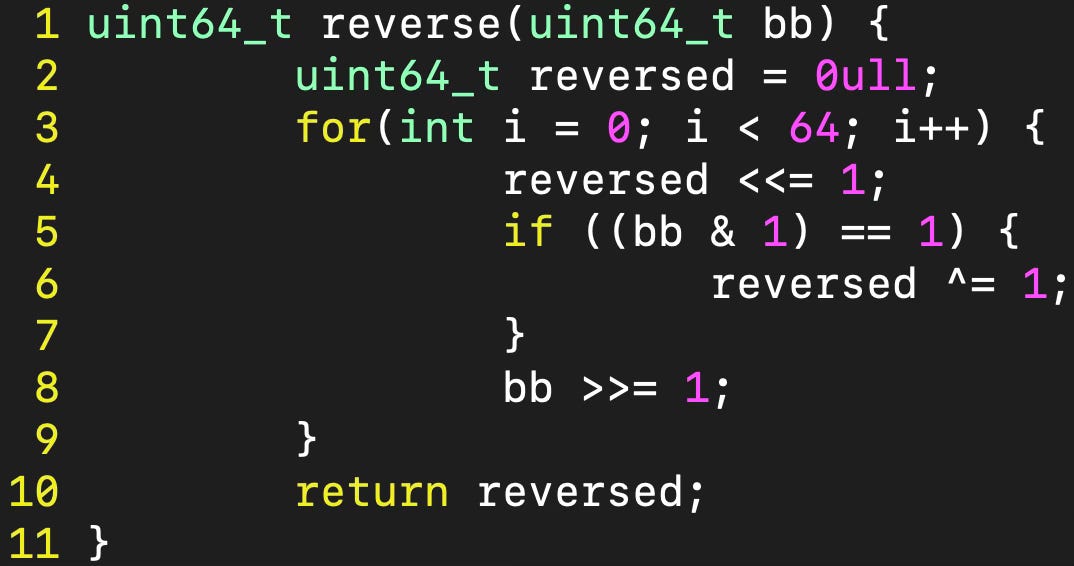
First, I wrote a function to reverse a bitboard:
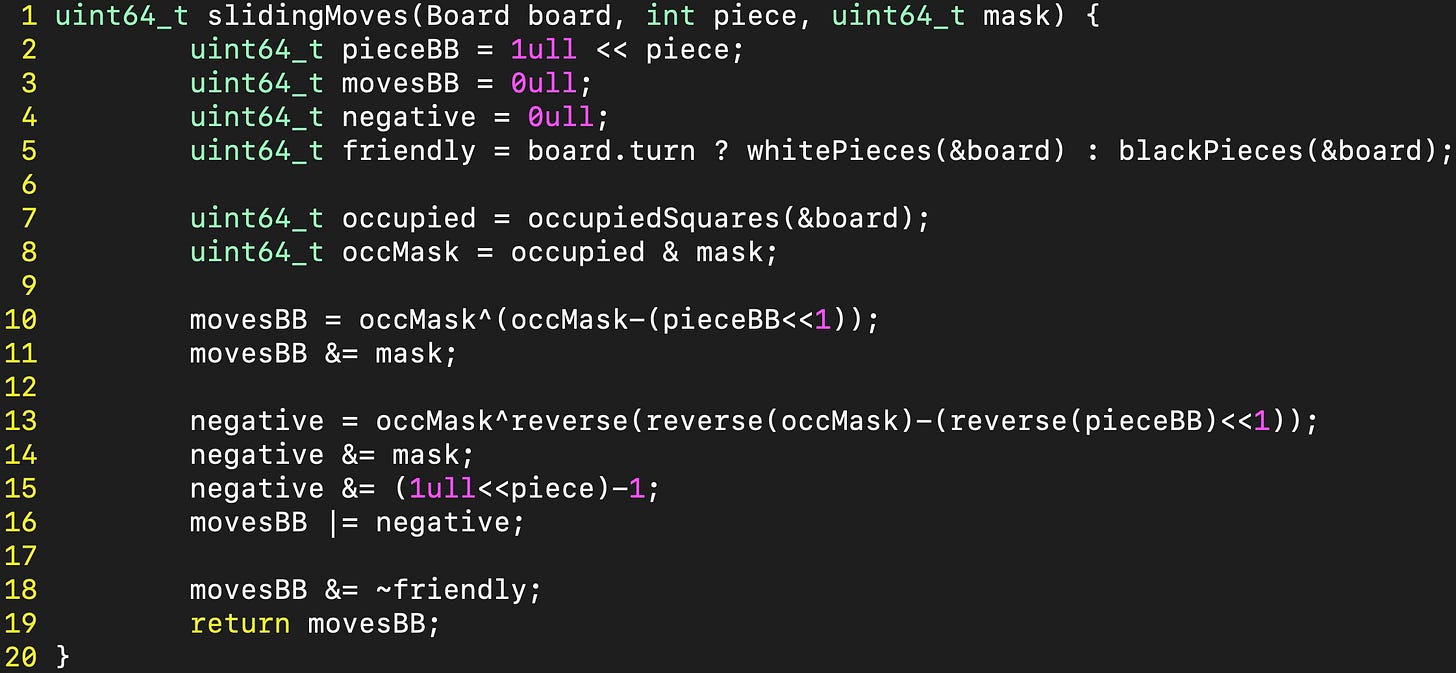
Since the operations work the same for files, ranks and diagonals, I wrote one function that performs these calculations and takes a mask as a parameter, which is the current file, rank or diagonal:
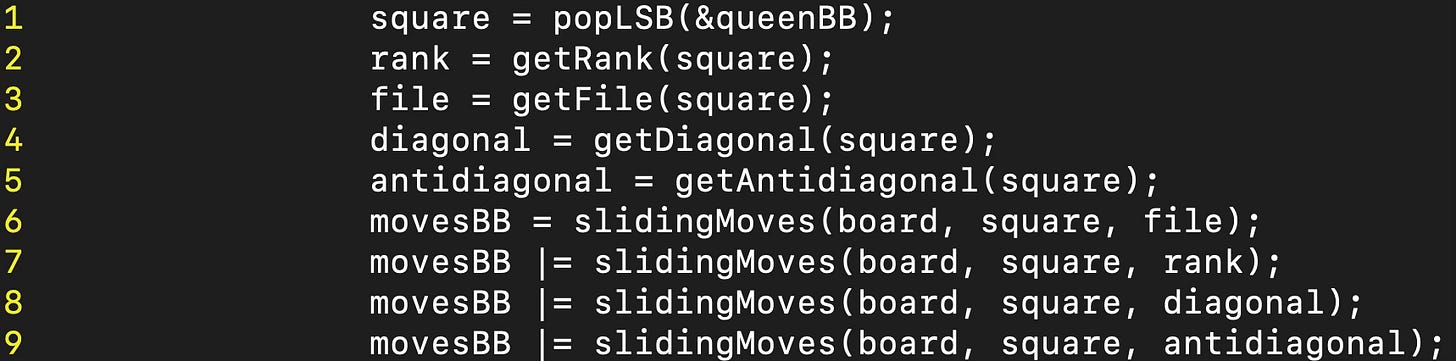
To generate the bitboard with the moves for a given piece, one uses the function from above for a specific file and rank (or diagonals). Here is the implementation of this for queens:
Finally, one needs to extract the actual moves from the bitboard, which is done the same way as for knights and pawns:
Next steps
I thought that move generation would take quite a bit of time, but I still underestimated it a bit. The castling moves are still missing from the generation and the moves still don't get played on the board. Also I need to test the whole code since a few bugs will probably have slipped in while writing all the code.
I hope that I'll get this done for next week, until then you can check out the source code if you're interested in the details of my implementation.