After working on the board representation, it's time to tell the engine how to move the pieces. If you're following along with the code, I added many helper functions to the board and bitboard classes, so check it out if you are interested.
Move encoding
Before generating moves, we have to decide on a way to represent the moves internally. Moves are best described by the start square of the piece, the square where it moves to and if it's a promotion, the piece to which the pawn got promoted to.
Since there are 64 squares, one needs 12 bits (64=2^6) to represent the start and end squares. Also there are 4 pieces to which a pawn can promote and with the additional option that the move is no promotion, one needs 3 bits to represent the promotion information. So I used a 16 bit number to represent the moves which is encoded as follows:
The start square in the example is 110101=53, which is the index of the c7-square, the end square is 111101=61, which is the index of the c8-square and the promotion piece is 100=4, which is a queen. So the move is from c7 to c8 and a promotion to a queen.
Note that we don't need to store the piece which moved, since there is only one piece on the starting square.
This encoding has one bit left over, which I might use later but for now I don't think that it's needed.
Move generation
There are two main ways to generate moves, one is to generate legal moves and the other method is to generate pseudo-legal moves.
Legal move generation is what you would expect, it only generates moves that end in a valid chess position.
Pseudo-legal moves respect all the rules for piece movement, but this method might generate moves that leave the own king in check. So some of the generated moves might actually not be legal moves. The legality of the moves gets only checked later, usually when the move will be actually played.
I'll use pseudo-legal move generation for the engine, so for now I'm not concerned if the king is in check after a move has been made.
Implementation
The move generation is closely linked to the board representation and now we can use many of the advantages that bitboards offer us. The main operation used for generating moves is bit shifting, which shifts a binary number a certain number of places to the left or right. So for example, if we look at the number 1010 and shift it 2 places to the left, we get 101000 and if we shift it 1 place to the right we get 101. In C++ the operator for shifting bits to the left is << and a right shift is >>. So our examples from above would be 1010 << 2 and 1010 >> 1 in code.
These shifting operations are executed very quickly by processors, which makes the move generation much more efficient.
King
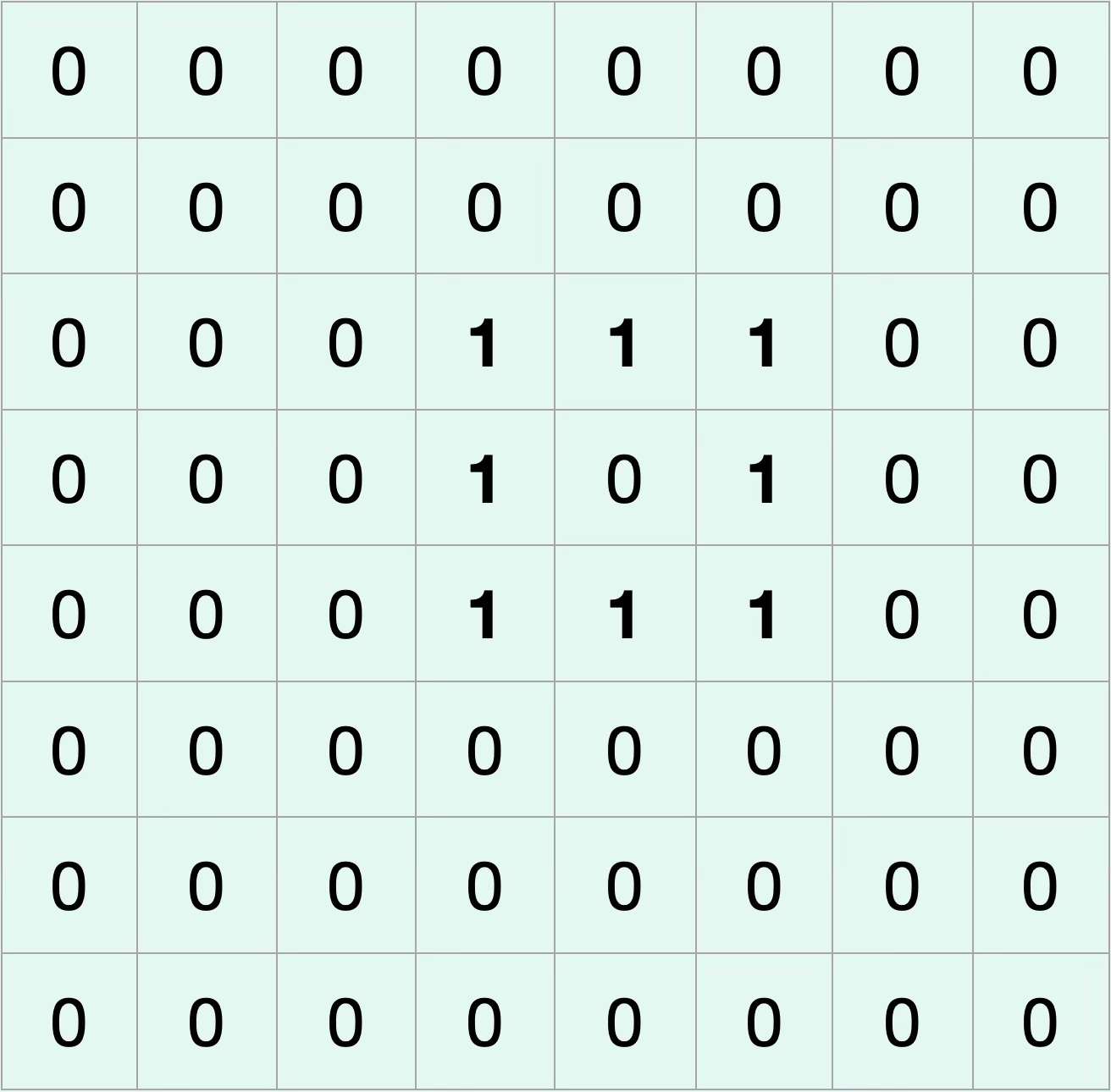
To see how this works in practice, let's start by looking at a lone king on the d5-square:
Here the king can move in all directions, so we want to get all the squares where the king can end up in order to generate the moves. If we want to get the square where the king moves left and up, which is the c6-square, we need to shift the bitboard that represents the king by 9 places to the left. Generating all possible king moves will give us the following bitboard:
This works well when the king is placed in the centre of the board, but if it's on the edge we have to take more care. To avoid that the king moves left when it's already standing on the a-file, we need to detect if the king is on the a-file before generating the moves. This is done by taking the bitboard for the a-file, inverting it and then ANDing the result with the bitboard of the king.
Since the AND operation is only 1 if both digits were a 1 before, the new bitboard will be empty if the king was standing on the a-file, otherwise it'll be unchanged.
The same is also done for the h-file and the first and eighth rank. I implemented this whole procedure as follows:
Now one has to also ensure that the king doesn't move to a square that is already occupied by a piece of the same colour.
This is similar to the situation where a king is on the edge of the board. This time we take the bitboard of the new squares for the king and the negated bitboard of the pieces of the same colour. These two get ANDed together and one is left with all squares that the king can move to which aren't occupied by its own pieces.
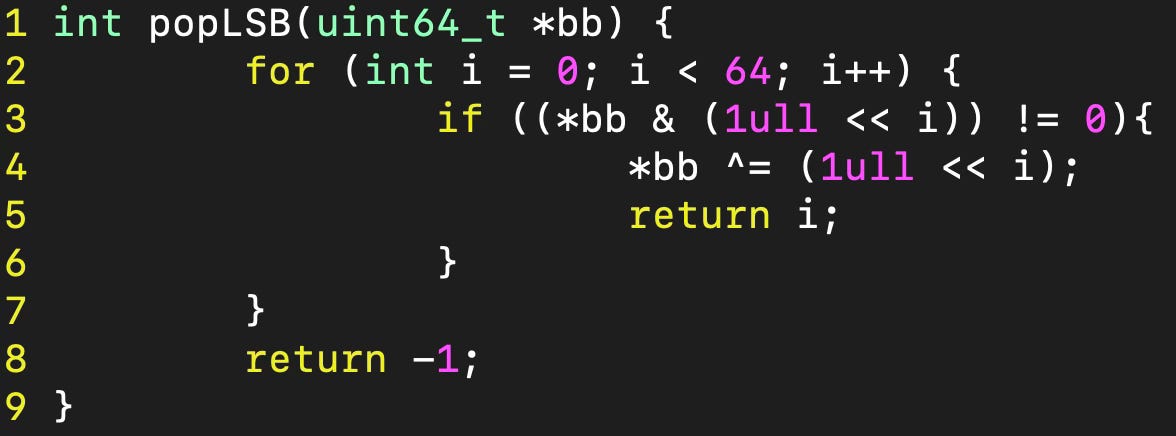
Finally, we need to get the moves from the bitboard with the possible future king position. To do this, I wrote a function that pops the least significant bit of a bitboard. This means that for 1010 it would return the index of the first 1 (read right to left) which is 1 (we start counting at 0) and it turns the original number into 1000.
With the bitboard of possible future king positions, this can be repeated as long as the bitboard isn't 0, at which point there aren't any moves for the king left. By doing this, we get the index end square for the different possible king moves. Together with the original square of the king, we can build the possible moves. This is implemented as follows:
Note that these moves might still contain illegal moves, like the king moving into check, since we are only generating pseudo-legal moves.
Knights
The move generation for the knights works very similar to the king. Since the knight can move to a set number of squares and isn't blocked by other pieces, the move generation is the same for the king, only with different values for the bit shifts and one was to be more careful with knights on the edge of the board.
The only thing that changes is that there can be multiple knights on the board at the same time. This can lead to problems where both knights can move to the same square and one has to create two moves for that square.
To deal with this, I again used the popLSB function to get each knight individually and place it on its own board. Then the move generation happens for one knight at a time.

Pawns
Pawns are more tricky to deal with. The biggest difference is that the movement of the pawns changes for the different colours. So one has to differentiate from the beginning between generating moves for White and Black. I wrote very similar code for both colours, making sure to switch the direction of the bitshifts. In the examples below, I'll only show the code for the White pawns.
Also, when pawns move normally, they can't take pieces of the opponent, while they are only allowed to move diagonally when they can capture a piece by the opponent. One also shouldn't forget en passant here.
And pawns are also allowed to move two squares on the first move, which is an additional rule and one has to be careful that the pawns won't "jump over" pieces on the third rank when implementing the double move.
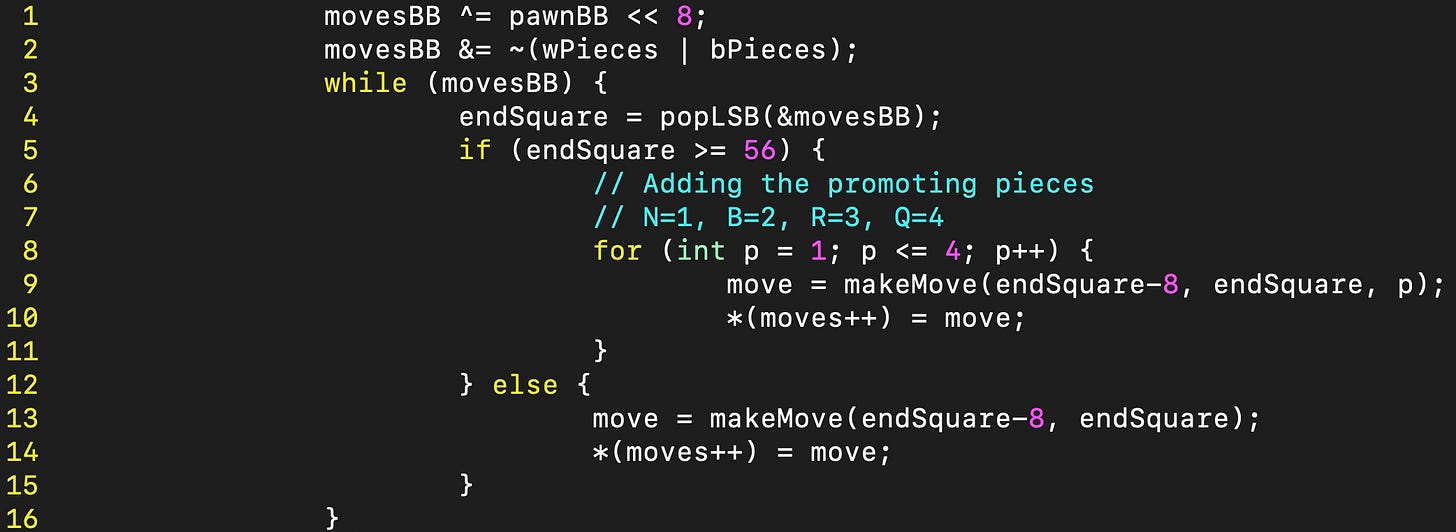
Let's start by looking at single pawn moves. To move the pawns, one simply needs to shift the bitboard by 8 digits to the left for White, or 8 digits to the right for black. Then one needs to check that the pawn landed on an empty square. Finally, one has to deal with promotions. I did this by checking if a pawn landed on the 8th (or first for Black) rank. If this is the case, I generated all possible promotions. Here is my code for this:
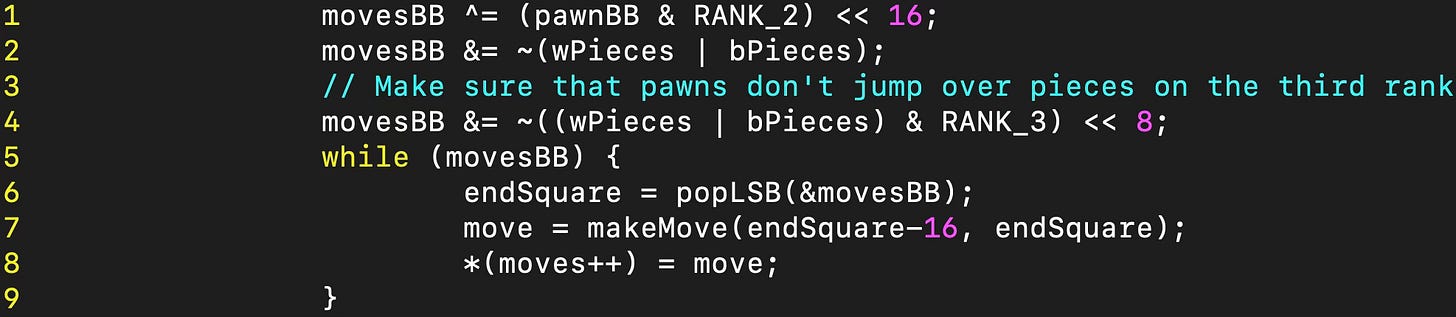
Double moves work similarly, but at first one has to ensure that only pawns on the second rank (seventh rank for Black) are considered. Also, it's important to check that the square on the directly in front of the pawn is empty to avoid that pawns jump over pieces. When looking at double moves, one doesn't have to consider promotions, since a pawn can't reach the last rank by a double move. The code looks as follows:
Note that until now we generated all pawn moves at once. This is more efficient and was possible because no two pawns could reach the same square when moving forwards. But when looking at captures, this changes slightly since two different pawns might be able to capture a piece on the same square.
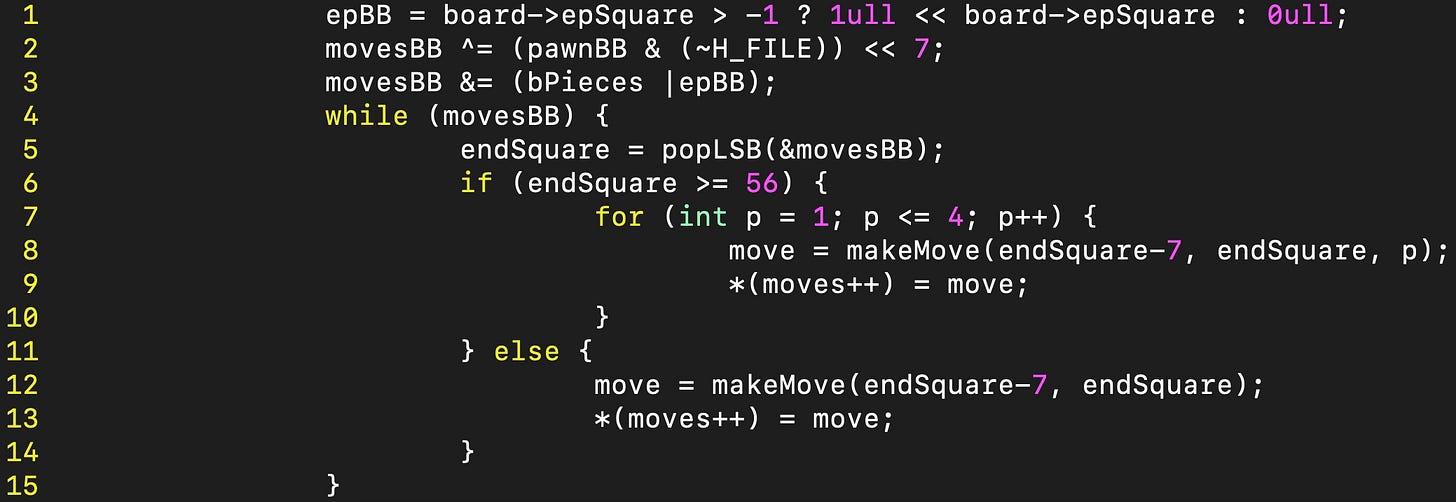
I dealt with this by first generating the captures to the right and then the captures to the left. One has to be careful to again clear the a- and h-files when necessary. When looking at captures, one has to ensure that there is actually an enemy piece on the square in order to make the move. One special case is en passant, which also has to be considered. Here is the code that implements the pawn captures to the right:
Next post
Next we have to deal with the remaining pieces, which are the sliding pieces, bishops, rooks and queens. There the move generation will be a bit more tricky, since the pieces can be blocked along the way of their movement (similar to pawns moving two squares). Castling also has to be implemented, but this shouldn't be too difficult since the castling rights are stored in the Board class. All of this will be the topic of the post next week.
Final remarks
I didn't expect that this post would be so long but I wanted to explain the move generation in some detail, since there are many subtleties involved. I also tried to show my implementation of all the important bits in code.
Let me know what you think of the length and depth of explanation of the post. I'm always happy to hear feedback.