Expected Scores for Chess Positions

Using Maia and LC0's WDL contempt to calculate expected scores

When looking at equal positions with engines, it's often quite hard to figure out which move to play. There might be many moves that lead to a draw, but since humans don't play perfect chess, some moves will offer more winning chances than others. So when playing a game, you might ask yourself which move has the highest expected score.

It's quite easy to get this information for openings. One can simply take a look at the Lichess opening explorer for the relevant rating range and see how well the opening scores. However, this approach can't be used for middlegames or endgames, since there are usually no games for that specific position in the database.

While thinking about this, I asked myself how well engines might predict the expected score between humans. Using Stockfish wouldn't work since it's way too strong. Specifically, the expected score should be adapted to different rating ranges. There are two engine approaches that came to mind for me, namely Maia and the WDL contempt feature of LC0.

Maia

The goal behind the Maia project was to create a chess engine that could predict human moves better than current engines. They managed to achieve this and published their models for different rating ranges as weight files that can be used with the LC0 engine.

Since the concept worked so well for predicting moves, I thought that the WDL (win, draw, and loss percentages) for a position might be a good predictor for the scores in human games.

LC0 WDL Contempt

The WDL contempt feature of LC0 can be used to specify the ratings of the players to LC0. I've mainly seen it used for opening preparation, where it produces extremely interesting ideas when you say that there is a big rating difference between the two players. GM Matthew Sadler has made some great videos about it.

I also played with this feature for a while, but only recently did I think about setting the rating difference to 0, meaning that both players have the same strength. As far as I understand, the WDL should then reflect that the game is played between two players, say with a rating of 2000, meaning that in general draw rates will be much lower compared to engine games and slightly difficult positions, which would objectively be equal, might be evaluated as an advantage for one side.

I used the following options for LC0 to set up the WDL contempt:

WDLCalibrationElo:  2000
Contempt:           0
ContemptMode:       white_side_analysis
WDLEvalObjectivity: 1.0
ScoreType:          WDL_mu

Comparing the WDL to real games

To see if the two engine predictions for the WDL come close to the score of real games, I decided to look at different opening positions and get the scores from the Lichess explorer. I used the Lichess API to get the data from the explorer and looked at different rating ranges.

I started by looking at ratings around 2000 on Lichess. I searched games with the rating option of 1800 and 2000 (which includes games from 1800-2199), used the Maia network trained on 1900-rated players, and set the WDL calibration Elo to 2000.

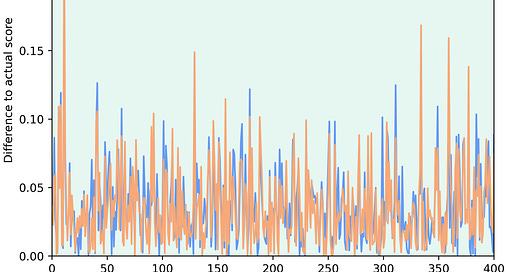
I was mainly interested in how the predicted scores of the engines differ from the actual results in the Lichess opening explorer. I looked at over 400 opening positions that had at least 500 games in the opening explorer. I plotted the absolute differences between the scores and got the following graph:

The difference in actual score and expected score for each position

The first striking thing for me is that the graphs for Leela and Maia mostly agree, which is kind of amazing since they work quite differently. Also, there is a lot of variation between different positions, with some very big spikes. The largest spike comes from the following position:

White to move

The engines say that the game should be equal (which is objectively true) but in practice Black scores very well from here on Lichess. This would indicate that the engines don’t capture all the points that make positions difficult to play for humans. But at the same time, most expected scores were much closer to the actual score of the game.

Since the graph is quite difficult to interpret, I also looked at the median and averages of the absolute differences from the actual scores.

So when looking at the expected scores with the engines, they are on average around 3% off the actual score, which is not that much.

I also looked at the 1500 rating level and got very similar results. Again, there were a few spikes in the graph and on average the engines were about 3% off the actual score. Also, Maia outperformed Leela in both rating ranges, but the WDL contempt feature has one big advantage to Maia, namely that one can choose an arbitrary rating for the WDL calibration Elo. So I also decided to give it a go for games by higher-rated players.

I looked at games by players on Lichess rated 2500+ and set the WDL calibration Elo to 2500. Looking again at the absolute differences in scores, I got the following graph:

Again, the graph is very similar to the one above and also the average is around 3.5% again.

Conclusion

One thing to note is that only looking at opening positions might be a bit of a flaw in the methodology, but since I needed to look at positions that occurred very often in actual games, I had no other choice. I would guess that most positions that occur that often are rather balanced, which might also influence the results.

Having said all this, the WDL contempt feature and the Maia networks are really interesting. I think that if you are unsure what to play in a position with many different possibilities, it might be worth looking at these engines for options that might capture human play better.