Calculating Piece Activity
An attempt at quantifying the piece activity in individual positions and games
One part I find always very intriguing about chess is piece activity. When watching great attacking games, it seems to be the most important factor in a chess position. But I always find it hard to quantify piece activity and weigh it against different factors in a position.
As always, I'd like to try and quantify concepts which are often talked about but never clearly defined. So I tried my hand at piece activity and looked at some games through the lens of my activity definition.
Defining Piece Activity
In principle, piece activity shouldn't be too difficult to define. After all, piece activity is closely related to the number of possible moves a piece has. However, the type of squares a piece controls is also important. A rook that covers the first rank is much less active than a rook on the seventh rank.
For my score, I started with counting all the legal moves of the pieces. I feel that this is a good starting point, but I also wanted to make sure that a piece which controls more important squares will also be considered more active. So I counted the attacked squares in the opponent's half double. I also counted the attacked squares adjacent the opponent's king a third time, to increase the activity of pieces aiming at the king. The final formula for each piece is
Piece Activity = (Attacked Squares) + (Attacked Squares in Opponent's Half) +
(Attacked Squares around Opponent's King)
The activity of a position is the sum of the individual activity of each piece (not counting pawns).
There are many tweaks that could be made. For example, one could increase the zone around the opponent's king where the squares are deemed to be more important. Or one could value central squares higher. And an even more detailed approach would be to tailor the formula for each type of piece, like counting rooks on the 7th rank as more active.
I decided to keep the formula simple for now but I might change it in the future. As always, it's difficult to say which formula would be more correct, but I certainly think that there is room for improvement. I'm interested to hear some suggestions from you about the formula.
Piece Activity in Games
As some of you will know by now, I like to use such scores to get a better overview of chess games. So the first thing I did was that I looked at how the piece activity developed in different games.
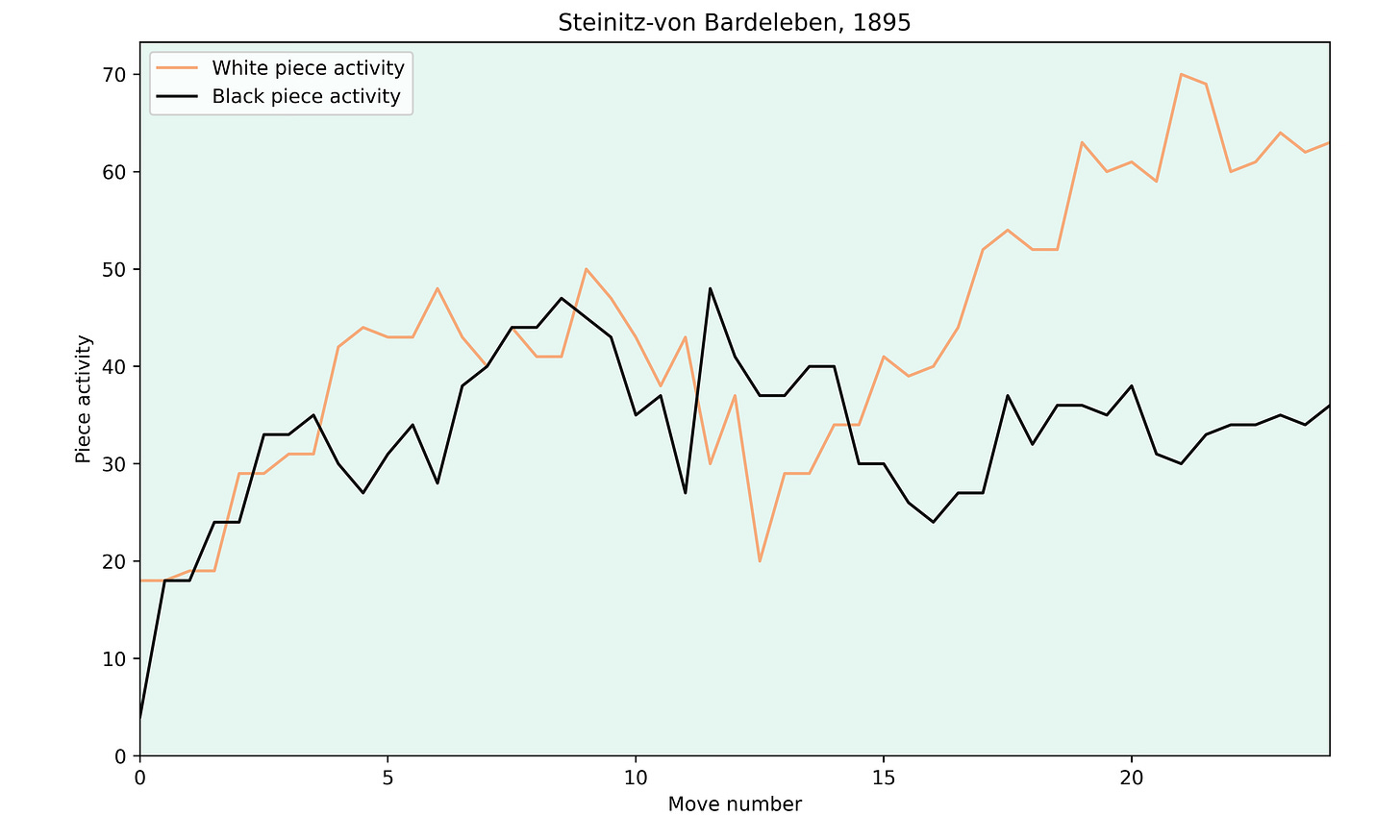
Firstly, I decided to look at the classic game Steinitz-von Bardeleben, 1895. I was mainly interested in the pawn sacrifice which Steinitz played on move 17:
Here Steinitz played 17.d5!. With this move, he cleared the d4-square to bring the knight into the attack and opened the c-file for his rook. Here is how the piece activity for both sides looks for this game:
It's clear to see how much the activity of Steinitz' pieces increased after move 17.
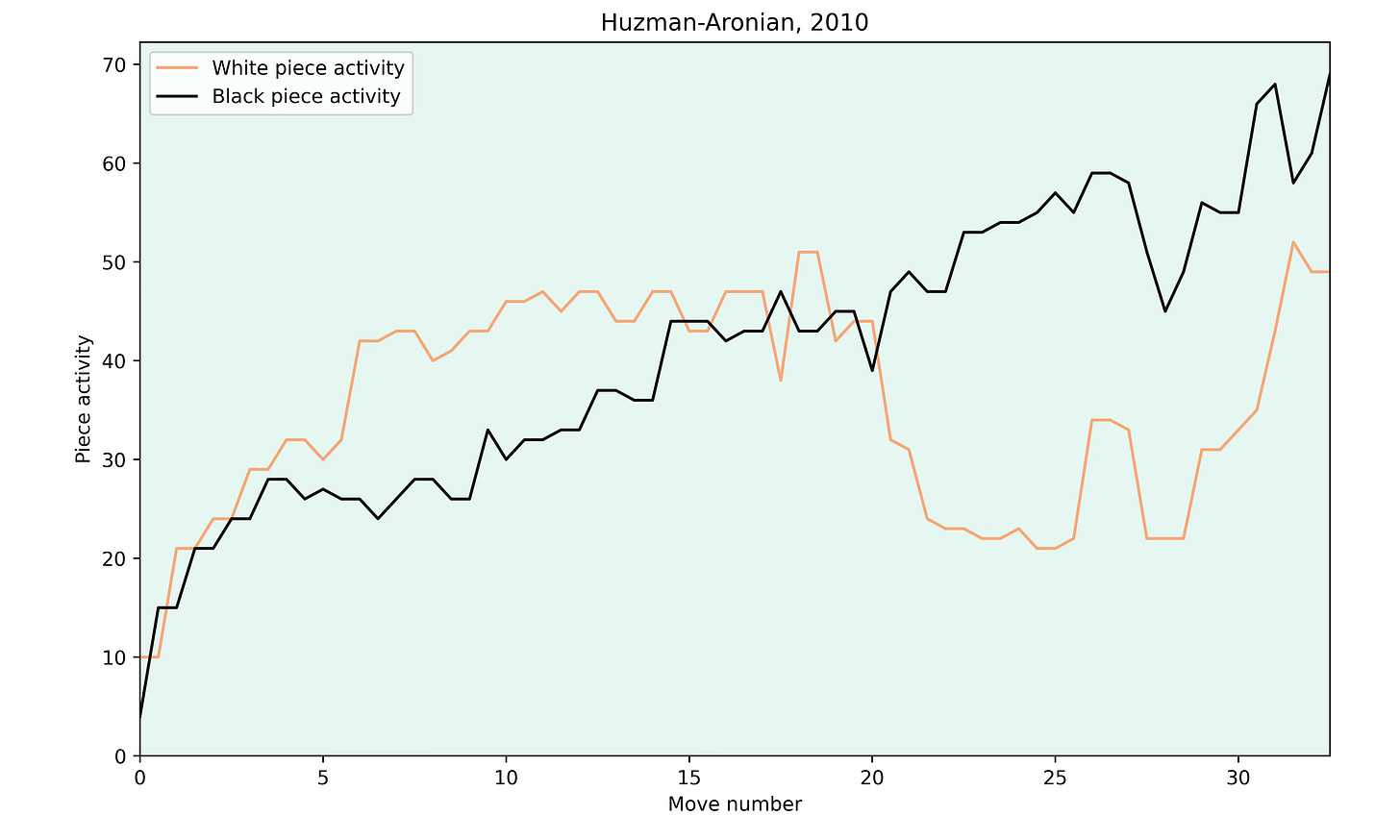
Another pawn sacrifice that came to mind was from the game Huzman-Aronian, 2010.
Aronian played 20…d4! in this position. This time the sacrifice not only increased the range of Aronian's pieces, but the white pawn on d4 also blocked the movement of the white pieces. This can be seen in the activity graph of the game:
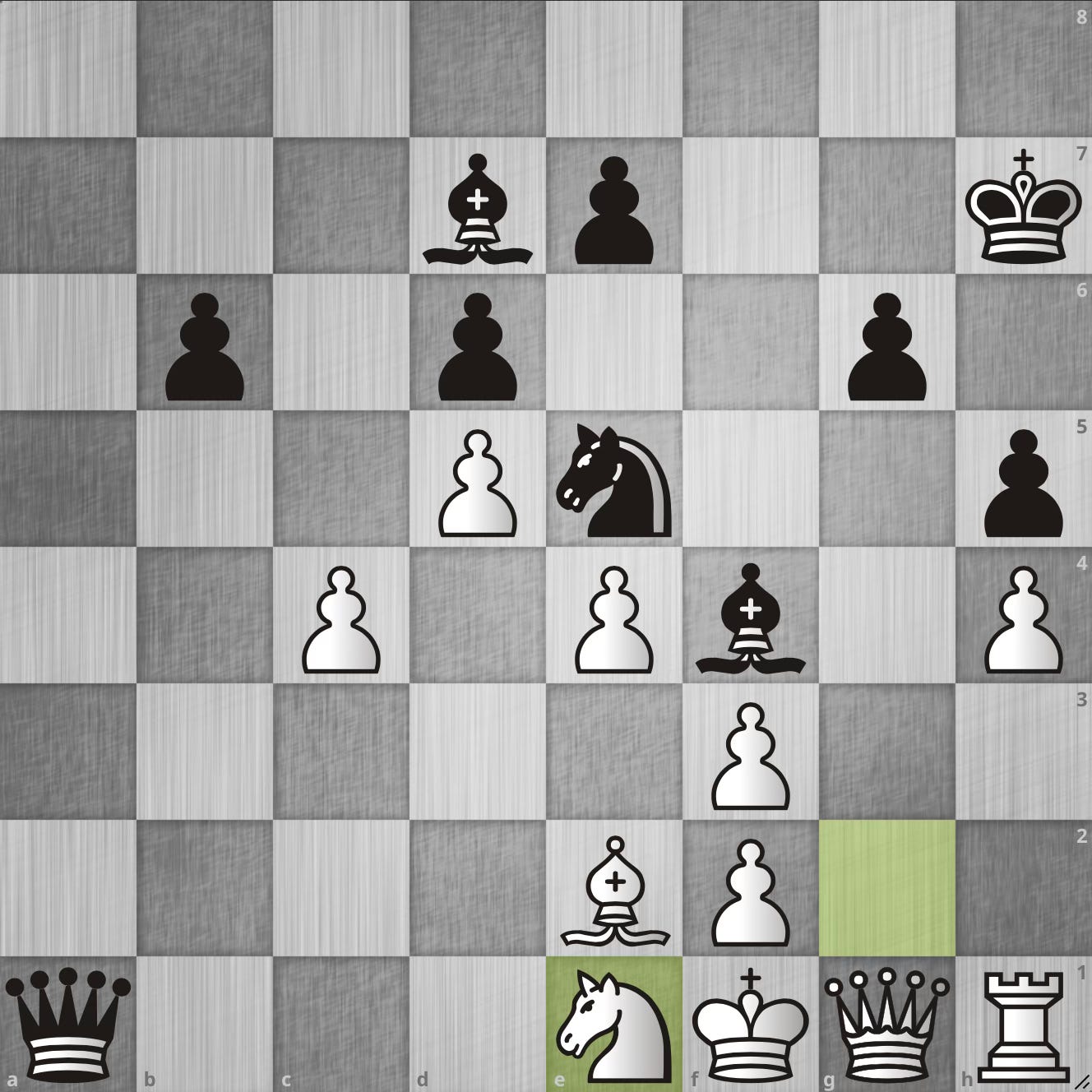
Finally, I thought that it would also be interesting to look at a game where one player restricted their opponent. The first game that came to mind was Fedoseev-Carlsen, 2021. Carlsen played a beautiful game and after 30 moves, they reached the following position:
All white pieces are stuck in the corner and Black is just dominating. This can also be seen from the piece activity plot for the game:
Around move 22, White's activity is steadily decreasing and the score is below 20 from then on. This score is not only much lower than the score of the black pieces, it’s also the lowest from all the games I looked at.
Future Ideas
One interesting question is how the activity relates to pawn sacrifices. It would be interesting to look at many different pawn sacrifices and see if there is a rough estimate of how much the activity score should increase to offer compensation for the pawn.
The current score has also big jumps when pieces are traded. It might make more sense to take the number of pieces into account to normalise the score and try to avoid these jumps. With this change, different types of positions might also be directly comparable.
As always, I'm very interested to hear any suggestions or ideas from you.





I teach along these lines, to consider net difference in activity as a higher-level version of Makogonov's famous rule "Improve the position of your worst-placed piece". Often exchanging an opponent's best piece, or preventing significant improvement of an opponent's piece is the most effective way to increase net difference in activity than to improve one's own piece activity.
(Attacked Squares) + (Attacked Squares in Opponent's Half) +
(Attacked Squares around Opponent's King)
I like these components. This artcle stimulates me to keep working on a more abstract versoin of piece activity, let's say potential activity. But if one were to get a derived version for a full legal position, then I do think these notions would be pressure components to include. not done reading. I hope this will be on lichess, too. I think you are doing exactly the kind of chess theory I thought has been missing.
As these are measure one would apply not in the one play mode games, not as such, but for chess study and theories of chess study (learning). many heads at it, and many games characterisation not necessary bound to the single game decision sequence problem on one indidivual, but putting some structure in the accumluating databases for high level concept to be better defined and shareable without having to be first an expert to talk about the same things. This is not going to make anyone having knowledge advantage in their own improvement track vision of chess, well it might if we the many start digested the accumulated data, for its emerging "logic". Eventually having other means to pull on the mass of data than which first moves got to a specific position, would allow some more theories of learning to be developped, (it might need other types of scientific sources or well definted models of the learner "mechanisms") and then maybe more rational ways of extending existing thoeries of conscious learning, into more conscious theories of subsoncsious learning, The experience does not have to be headless chicken random picking, that might spuriously cluster (if we had no such metrics or components metrics to characterize expeirence). What would unifrom random even mean.